
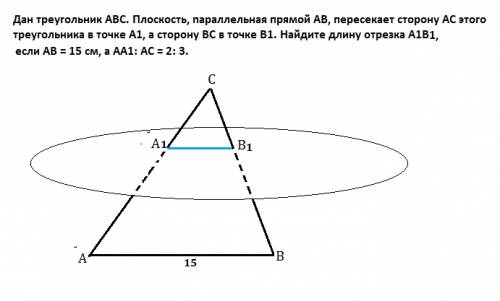
По одной из формул: площадь треугольника равна половине произведения длин его сторон на синус угла между ними.
При пересечении диагоналей вертикальные углы равны.
Пусть ∠АОВ=∠DOC=α Тогда смежные им ∠DOA=∠BOC=180°- α. sinα=sin(180°- α)
Примем АО=а, ВО=b, СО=с, DO=d. Тогда:
S(AOB)=a•b•sinα/2
Ѕ(DOC)=d•c•sinα/2
S(AOB)•Ѕ(DOC)=a•b•c•d•sin²α/4
S(AOD)=a•d•sinα/2
S(BOC)=b•c•sinα /2
S(AOD)•S(BOC)=a•d•b•c•sin²α/4
a•b•c•d•sin²α/4 =a•d•b•c•sin²α/4 ⇒
S(AOB)•Ѕ(DOC)= S(AOD)•S(BOC), что и требовалось доказать.
ответ: r = 5*(4+√5)/11
Объяснение:
A,B,С - точки касания внутренних окружностей с внешней
O1,O2,O3 - центры внутренних окружностей
O-центр внешней окружности. (смотрите рисунок)
O1S- высота
r- радиус красной окружности
Из условий касания окружностей и симметрии имеем :
O1O=5-r
O1O2 =O1O3 = 2+r
O2S=O3S=2
OO2=OO3= 5-2 = 3
По теореме Пифагора:
OS = √(3^2- 2^2) = √5
O1S = 5+√5 -r
По теореме Пифагора:
(5+√5 -r)^2 = (2+r)^2 - 2^2
(2+r)^2 - (5+√5 -r)^2 = 4
(7+√5)*( -3-√5+2r) =4
-3-√5+2r = 4/(7+√5) = 4*(7-√5)/44 = (7-√5)/11
-33 - 11√5 +22r = 7-√5
22r = 40 +10√5
r = (20+5√5)/11 = 5*(4+√5)/11