площадь трапеции
площадь трапеции равна произведению полусуммы ее оснований на высоту:
s = ((ad + bc) / 2) · bh,
где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
доказательство.

рассмотрим трапецию abcd с основаниями ad и bc, высотой bh и площадью s.
докажем, что s = ((ad + bc) / 2) · bh.
диагональ bd разделяет трапецию на два треугольника abd и bcd, поэтому s = sabd + sbcd. примем отрезки ad и bh за основание и высоту треугольника abd, а отрезки bcи dh1 за основание и высоту треугольника bcd. тогда
sabc = ad · bh / 2, sbcd = bc · dh1.
так как dh1 = bh, то sbcd = bc · bh / 2.
таким образом,
s = ad · bh / 2 + bc · bh = ((ad + bc) / 2) · bh.это можно только с доказательством
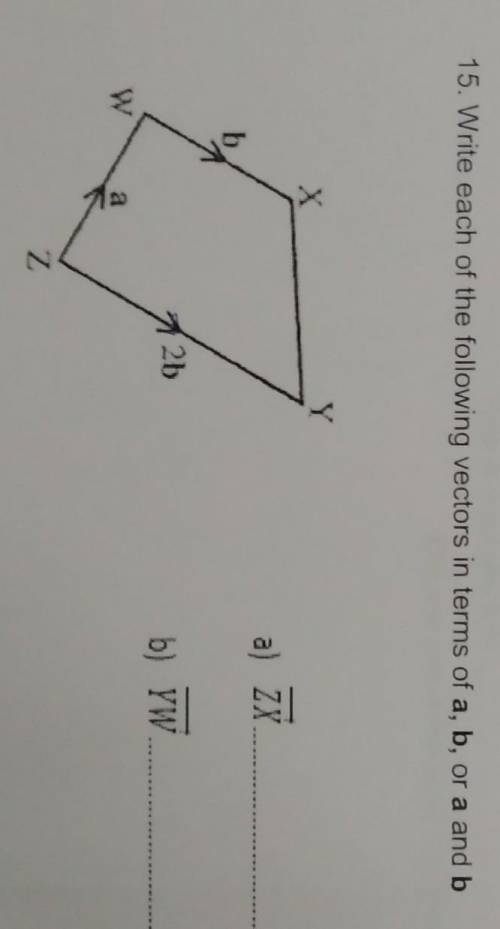
1) вектор ZX=b-a
2)вектор YW=a-2b
Разность векторов можно нахо
дить по правилу параллелог-
рамма.
Шаг 1:
С параллельного пе
реноса располагем заданные
векторы так, чтобы они исходи
ли из одной точки (совмещаем
их начала).
Шаг 2:
На этих двух векторах достраи
ваем параллелограмм.
Шаг 3:
Соединяем концы векторов
(в построенном параллелог
рамме это его меньшая диа
гональ).
Шаг 4:
Осталось определить направ
ление искомого вектора.
Вектор разности соединяет
концы вычитаемых векторов
и напрвлен к тому вектору, от
которого отнимают ( при усло
вии, что вектора иходят из од
ной точки).