
Даны : А(2,1,0), М(3,-2,1), N(2,-3,0).
Находим координаты направляющего вектора прямой NM:
NM: (1; 1; 1).
Принимаем координаты направляющего вектора прямой NM как соответствующие координаты нормального вектора n плоскости α :
n = (A; B; C). То есть, A = 1, B = 1, C = 1.
Записываем уравнение плоскости, проходящей через точку А(2; 1; 0) и имеющей нормальный вектор n(A; B; C), в виде:
A(x -x1) + B(y - y1) + C(z - x1) - это и есть искомое уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Подставляем данные -
α: 1(x -2) + 1(y - 1) + 1z = x + y + z - 3 = 0.
ответ: уравнение плоскости α: x + y + z - 3 = 0.
ширина проёма ключа=25√3+1≈44,25мм
Объяснение:
Проведём диагонали СК и ВЕ и обозначим точку их пересечения О, которая также является центром вписанной окружности. Проведём 2 радиуса ОР и ОН. Радиус вписанной окружности в правильном шестиграннике вычисляется по формуле:
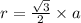
где а - любая сторона шестигранника.
Подставим в эту формулу наши данные:
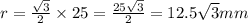
Ширина проёма ключа - это диаметр шестигранника РН+2×0,5мм зазора.
Поскольку диаметр - это 2 радиуса, то
РН=12,5√3×2=25√3мм
Зазор - это продолжение диаметра на 0,5мм от каждой из двух сторон шестигранника, поэтому зазор с двух сторон составит:
2×0,5мм=1мм
Тогда ширина проёма ключа равна 25√3+1
Можно так и оставить, но если нужно вычислить полностью, тогда √3≈1,73, и подставим это значение вместо корня:
25×1,73+1=43,25+1=44,25мм
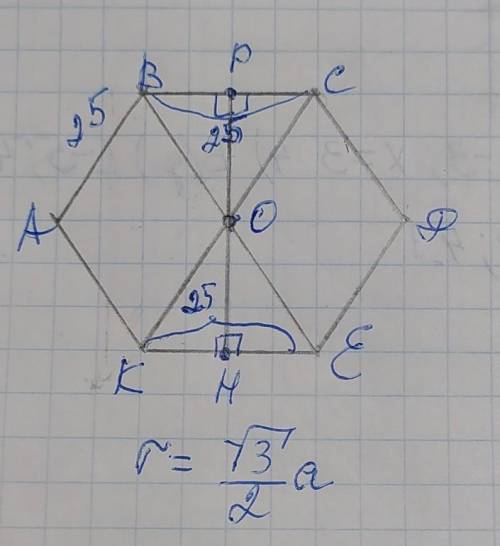
Объяснение:
AO можно найти из прямоугольного треугольника AOB (∠ABO=90°).
Однако сначала найдем ∠AOB:
(здесь l - длина меньшей дуги BC, R=OB)
Переведем полученное значение в радианы:
Так, получили, что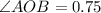 .
.
Из треугольника AOB:
Тогда:
Задача решена!