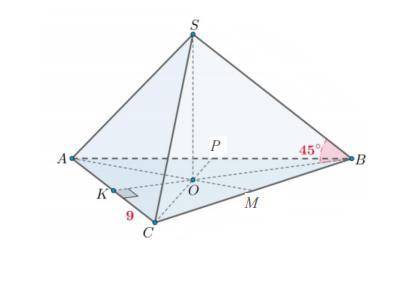
Объем пирамиды равен произведению трети высоты SO на площадь основания -равнобедренного треугольника АВС с основанием АС . Зная основание, можно найти сторону КВ=√(ВС²-КС²)=√(100-81)=√19, площадь основания равна 9*√19/см²/, по свойству медиан, они пересекаются в отношении 2/1, считая от вершины, получим ОВ=2ВК/3=2√19/3, т.к. ребро SB наклонено к плоскости основания под углом 45°, то SO=OB=2√19/3, окончательно, объем пирамиды равен (1/3)*9*√19*2√19/3=38
Площадь боковой поверхности цилиндра:
Sбок = 2πRH
По условию H = R - 2,
2πR(R - 2) = 160π
R(R - 2) = 80
R² - 2R - 80 = 0 по тоереме Виета:
R = 10 или R = - 8 (не подходит по смыслу задачи)
Н = R - 2 = 8 см
а) Осевое сечение - прямоугольник, стороны которого равны диаметру основания и высоте цилиндра:
Sос. сеч. = 2R · H = 2 · 10 · 8 = 160 см²
б) Сечение цилинра, параллельное оси, имеет форму прямоугольника, одна сторона которого равна высоте. Найдем другую сторону (АВ).
ΔАОВ равнобедренный (АО = ВО как радиусы). Проведем ОС⊥АВ, ОС = 6 см по условию. ОС является так же медианой, ⇒ АС = ВС.
ΔАОС: ∠АСО = 90°, по теореме Пифагора:
АС = √(АО² - ОС²) = √(10² - 6²) = √(100 - 36) = √64 = 8 см
АВ = 2АС = 16 см
Sсеч = AB · H = 16 · 8 = 128 см²
V=1/3Sосн×h
V=1/3Sосн×SO
AC=AK+KC=3+9=18(см)
AP=PB=1/2AB=5(см)
CM=MB=1/2BC=5(см)
Pосн=18+10+10=38(см)
p=38/2=19(см)
Sосн=√p(p-AB)(p-BC)(p-AC) =√19(19-10)(19-10)(19-18)=√19×9×9×1=9√19(см²)
С треугольника BKC(K=90°)
KB²=BC²-KC²
KB²=100-81=19
KB=√19(см)
OB=1/2√19(см)
С треугольника SOB(O=90°)
tg45°=SO/OB
1=SO/√19
SO=√19
V=1/3×9√19×√19=57(см³)