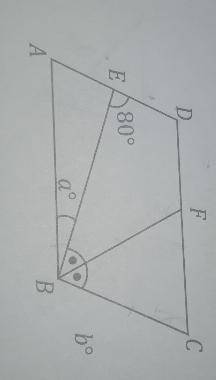
ответ: ВМ=22
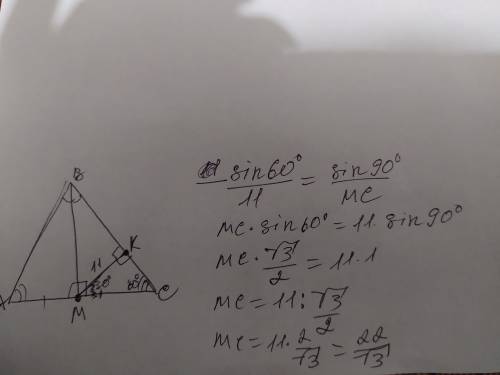
Объяснение: обозначим прямую от точки М до стороны ВС - МК=11 высотой стороны ВС. У нас получился прямоугольный треугольник МСК, в котором угол С =60°(по условиям, поскольку ∆АВС равносторонний). В ∆МСК угол СМК=30°(180-90-60). Теперь применим теорему синусов и найдём сторону МС: теорема синусов на фото ниже
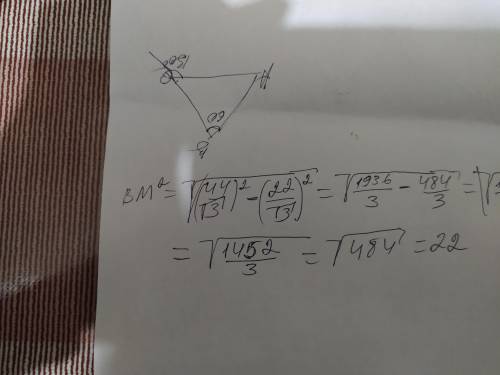
В ∆СВМ угол СВМ=30°(по условиям, поскольку медиана проведённая из вершины В является ещё биссектрисой, которая делит угол пополам и высотой. В прямоугольном ∆СВМ сторона ВС=22/√3×2=44√3(по свойствам угла 30°- катет, лежащий напротив угла 30°=половине гипотенузы). Теперь по теореме Пифагора ВМ= решение по теореме Пифагора на фото ниже
Аксиома 1
Через две точки можно провести прямую линию и притом только одну.
Аксиома 2
Если две точки прямой принадлежат плоскости, то и каждая точка этой прямой принадлежит плоскости.
Аксиома 3
Отрезок прямой короче всякой другой линии (ломаной или кривой), соединяющей его концы.
Расстояние между двумя точками измеряется по прямой линии. В геометрии используются еще и такие аксиомы, которые уже применялись в арифметике и алгебре (сформулируем их для произвольных величин A, B и C):
Аксиома 4
Если A=B и B=C, то A=C.
Аксиома 5
Если A=B, то A+C=B+C и A-C=B-C.
Объяснение:
здесь ответы