на сторонах bc и cd параллелограмма abcd отметили соответственно точки F и E так , что BF:FC= 0,5 , DE: EC=0,75.Прямые FD и AE пересекаются в точке M.Найдите отношение FM:MD
Объяснение:
BF:FC= 1/2 , DE: EC=3/4.
Пусть ВС=а, DC=в. Тогда FC= 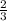 a
a
1) ΔFMY ≈ΔDMA по двум вертикальным углам и накрест лежащем при ВС║AD, AY-секущая : ∠FMY=DMA , ∠FYM=∠DAM.
В подобных треугольниках сходственные стороны пропорциональны 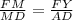 или
или 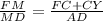 .
.
2) ΔCEY ≈ΔDEA по двум вертикальным углам и накрест лежащем :при ВС║AD, AY-секущая : ∠СEY=DEA , ∠CYE=∠EAD.
В подобных треугольниках сходственные стороны пропорциональны 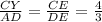 или CY=
или CY=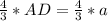
3) 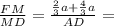
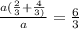 =
=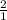
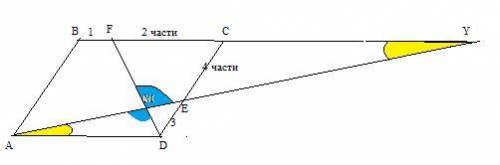
Картинка в этой задаче действительно желательна.
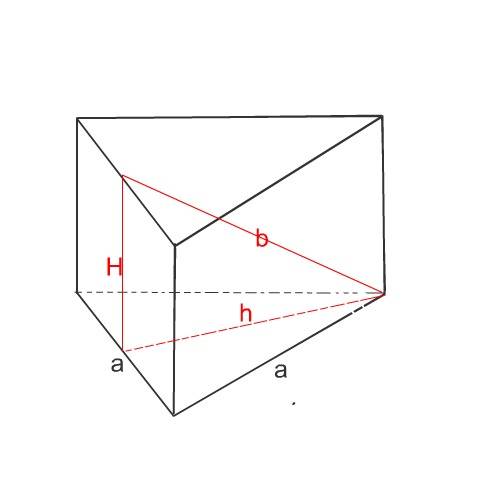
Объем правильной треугольной призмы равен произведению площади основания на высоту призмы.
Площадь основания - это площадь правильного треугольника со стороной а.
Формула площади равностороннего треугольника
S=(a²√3):4
Высоту призмы найдем из прямоугольного треугольника,
катеты в котором- высота призмы и высота треугольника=основания,
а гипотенуза - данное в условии расстояние b от вершины одного основания до противолежащей стороны другого основания.
Высота правильного треугольника находится по формуле
h=а√3):2
Высоту призмы найдем по теореме Пифагора:
Н= √(b²-h²)=√(b²-3а²:4)
V= (a²√3):4)·√(b²-3а²:4)
Если треугольники подобны, то каждая из подобных сторон большего треугольника меньше в n раз, чем у меньшего, значит и периметр большего тр. тоже меньше периметра меньшего в n раз, если предположить что сторона 3см подобна стороне 15см, то n=5, если сторна 7см подобна стороне 35 см, то n тоже=5, следовательно, что сторона 6см подобна третьей стороне то она равна 6*n=6*5=30, можно проверить через периметр. периметр меньшего треугольника равен 16см, а периметр большего получается равен 80см, 80:5=16. значит длина третьей стороны треугольника равна 30 см.
Объяснение: см. во вложении