ответ: 1 (ед. длины)
Объяснение:
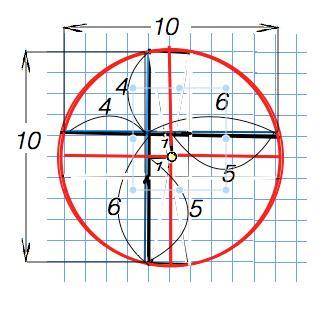
Чтобы найти расстояние от центра окружности до каждой хорды, проведем через середину каждой перпендикулярно по прямой. Прямая, проведенная перпендикулярно хорде через середину, проходит через центр окружности и содержит диаметр окружности ( свойство). При этом пересекающиеся хорды и пересекающиеся диаметры ( которые будут параллельны хордам и взаимно перпендикулярны) образуют квадратик со сторонами, равными разности между бóльшим отрезком, на которые хорды делятся при пересечении, и их половинами. Длина каждой хорды 6+4, их половин 10:2.
6 - (6+4):2 =1. (См. рисунок приложения)
Найдите положительное значение параметра t, при котором векторы
a = (t; 1 - t; 7), b = (t + 1; 2; - 2), заданные своими координатами в ортогональном базисе, ортогональны.
Объяснение:
Вектора a и b называются ортогональными, если угол между ними равен 90°.
Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю.
а*в=t(t+1)-2(1-t)-2*7 , t(t+1)+2(1-t)-2*7 =0
t²-t-16=0, D=49 , t₁=5 , t₂=-4 .
Положительное значение параметра : t=5.