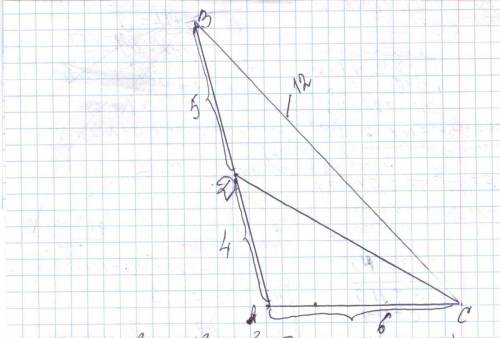
Дан треугольник ABC, у которого AB=9, ВС=12, AC=6. На стороне AB отложен отрезок AD = 4 , и точка D соединена отрезком прямой с вершиной С. Определите отрезок CD.
ответ: 8
Объяснение:
Теорема косинусов применим относительно ∆ABC и ∆ADC (или ∆BDC)
Из ∆ABC: BC² = AB² + AC² -2AB*AC*cos∠A (1)
12² =9² +6² -2*9*6*cos∠B ⇒ cos∠A = (9² +6²-12²) / 2*9*6 = - 1/4 ;
Из ∆ADC: DC² = AD² + AC² -2AD*AC*cos∠A (2)
DC² = 4² + 6² -2*4*6*(-1/4) ⇔ DC² = 64 ⇒ DC= 8.
= = = "Арифметика" (теорема стюарта) = = =
Из ∆ADC: AC² = DC² +AD²-2DC*AD*cos∠ADC ⇔
2DC*AD*cos∠ADC = DC² + AD² - AC² (*)
Из ∆ABC: BC² = DC² +BD²-2DC*BD*cos(180°-∠ADC) ⇔
2DC*BD*cos∠ADC = BC² - DC² - BD² (* *)
AD/BD =(DC² + AD² - AC²)/ (BC² - DC² - BD²)
4/5 =(DC² - 20 ) / (119 -DC²) ⇔476 - 4*DC² = 5*DC² - 100⇔
476 +100 = 5*DC²+ 4*DC² ⇔576 =9*DC²⇔DC²= 64
DC = 8
* * *CD²*AB =CA²*BD +CB²*AD -AB*AD*BD * * *
128
Объяснение:
1) Пусть точка D - середина ребра СС₁, а точка Е - середина ребра АВ.
ΔAСD = BCD (по двум катетам), следовательно, АD = BD и ΔАDB - равнобедренный, в силу чего DE как медиана равнобедренного треугольника перпендикулярна АВ.
2) Согласно 4-ому признаку равенства прямоугольных треугольников ΔВED = ΔВCD, т.к. катет ВЕ = катету DC= 8, а гипотенуза ВD у этих треугольников является общей стороной.
Следовательно, катет ЕD = катету ВС = 16.
3) Площадь сечения плоскостью, проходящей через прямую АВ и середину ребра СС₁, - это площадь треугольника ABD, которая равна половине произведения основания АВ на высоту ЕD:
S = АВ · ЕD : 2 = 16 · 16 : 2 = 256 : 2 = 128
ответ: 128
Объяснение:
Угол между скрещивающимися прямыми - это угол между прямыми, параллельными заданным и лежащими в одной плоскости.
Так как все ребра равны 1 ⇒ основания призм - равносторонние треугольники, боковые грани - квадраты.
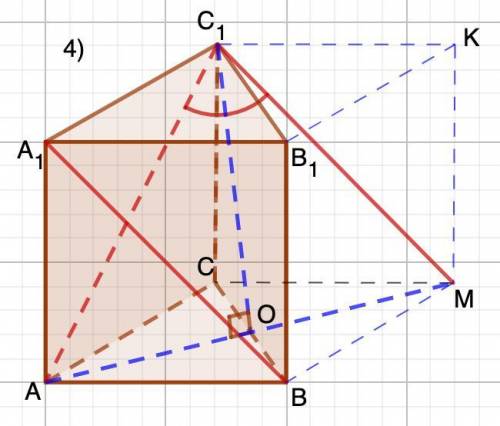
4) Достроим данную треугольную призму до четырехугольной. А₁В║С₁М. ⇒ Искомый ∠АС₁М.
По теореме Пифагора:
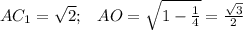

∠AC₁O=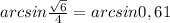 ≈37°
≈37°
⇒ ∠АС₁М ≈37°·2=74° (С₁О - высота, биссектриса равнобедренного ΔАС₁М )
5) A₁C₁║АС ⇒ искомый ∠АСВ₁ .
По теореме Пифагора:

В₁Н - высота, медиана.
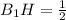
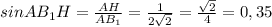
∠АВ₁Н=arcsin 0,35≈20°
⇒ ∠АВ₁С≈40° (В₁Н-высота, биссектриса равнобедренного ΔАВ₁С.)
∠В₁АС=∠АСВ₁=(180°-40°):2≈70°
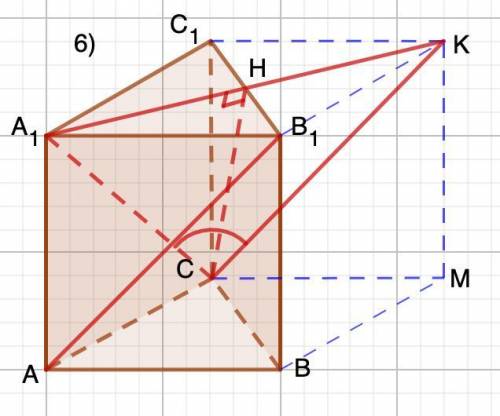
6) Достроим данную треугольную призму до четырехугольной. АВ₁║СК.
⇒ Искомый ∠А₁СК.
По теореме Пифагора:

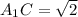
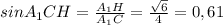
⇒ ∠А₁СН=arcsin 0,61≈37°
∠А₁СК≈74° (СН-высота, биссектриса)

=================================
Объяснение: