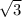

Уравнение окружности имеет вид :
(x - x₀)² + (y - y₀)² = R² ,
где x₀, y₀ - координаты центра окружности, R - радиус окружности
(x - 1)² + (y + 2)² = 1 ⇒ Центр окружности О(1; -2), радиус R=1
При симметрии относительно оси OY радиус и координата у не изменятся, а координата х поменяет знак
(x + 1)² + (y + 2)² = 1 ⇒ Центр окружности O₁(-1; -2), радиус R=1
При симметрии относительно оси OX радиус и координата х не изменятся, а координата у поменяет знак
(x - 1)² + (y - 2)² = 1 ⇒ Центр окружности O₂(1; 2), радиус R=1
При последовательной симметрии относительно осей ОX и OY (центральная симметрия) радиус не изменится, а обе координаты поменяют знаки
(x + 1)² + (y - 2)² = 1 ⇒ Центр окружности O₃(-1; 2), радиус R=1

Внутри правильного треугольника со стороной √3 выбрана произвольная точка . Чему равна сумма расстояний от этой точки до сторон треугольника ?
Объяснение:
Пусть точка Р-произвольная. Опустим на стороны правильного ΔАВС перпендикуляры . Обозначим их х,у,z ( кстати, получили педальный треугольник, если соединить основания перпендикуляров).
S(ABC)=S( PAB)+S(PBC)+S(PAC).
S(ABC)=S(равн. тр)=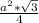 =
=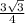 ,
,
S( PAB)=1/2*a*h=1/2*√3*x,
S(PBC)=1/2*a*h=1/2*√3*y,
S(PAC)=1/2*a*h=1/2*√3*z.
x+y+z=1,5