от вершины основания до центра описанной окружности 13, а проекция этого радиуса на основание равна 12.
Поэтому от центра описанной окружности до основания 5 (это заклинание 5,12,13:.
А целиком высота треугольника 13 + 5 = 18;
А вот дальше - ничего веселого, но тут уж ничего не поделать - числа не я подбирал.
Боковая сторона равна корень(18^2 + 12^2) = 6*корень(13);
периметр P = 12*корень(13) + 24 = 12*(корень(13) + 2);
площадь S = 24*18/2; оставим так пока
r = 2*S/P = 24*18/(12*(корень(13) + 2)) = 36/(корень(13) + 2);
упрощать это смысла нет. Это примерно 6,42220510185596, то есть треугольник очень близок к правильному, поскольку R - 2*r = 0,155589796288087, очень маленькая величина по сравнению с R = 13.
опять все просто - треугольник составлен из 2 "египетских" (точнее, ему подобных, со сторонами 9, 12 ,15, приставленных друг к другу катетами 12).
Поэтому высота 12, площадь 108, периметр 48, радиус вписанной окружности 2*108/48 = 9/2;
Радиус описанной окружности можно найти по формуле R = abc/4S, это элементарно. Продолжу-ка я высоту к стороне 18 за основание до пересечения с перпендикуляром к боковой стороне, проведенным через один из концов основания. Получившийся треугольник вписанный в окружность прямоугольный треугольник, его гипотенуза - диаметр. Из подобия треугольников легко получается
(2*R)/15 = 15/12; R = 225/24 = 75/8;
Любопытно отметить, что 2*r = 72/8; то есть разница R - 2*r = 3/8 - очень маленькая. Эта разность равна 0 в правильном треугольнике.
В графике A задана функция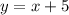 ;
;
В графике В задана функция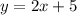 ;
;
В графике С задана функция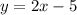 ;
;
В графике D задана функция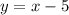
ответ: 1-С; 2-А; 3-В; 4-D