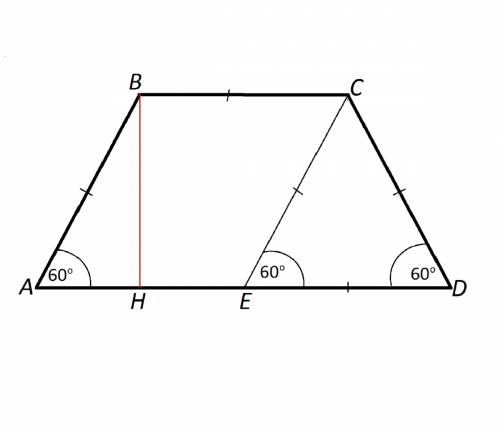
опускаем перпендикуляр из верхнех углов, они отсекают от нижней грани равные части, если верхняя основа = 6, 12-6=6, т.к. частей
этих 2, то делим на 2, значит одна из этих "отсекаемых" частей = 3. у нас получается треугольник, в котором, есть одно из этих частей нижней основы(3), нижний угол (60) и прямой угол (90), мы знаем что сумма углов треугольника равна 180, значит верхней угол будет = 180 - (60 +90)=30. за теоремой мы знаем что катет прямоугольного треугольника лежащий против 30 градусов, равен половине гепотенузы, а в нашем случаее это та самая отсекаемая часть (3), значит гипотенуза = 3 * 2 = 6. гипотенуза и есть боковая часть.
ответ боковая часть равно 6
В треугольнике, построенном при продолжении сторон, меньший острый угол равен 30°, тогда больший 60°, значит, большая боковая сторона лежит против угла в 60°, средняя линия равна полусумме оснований. Пусть х- неизвестное основание трапеции. 8√3/3=(х+4√3/3)/2⇒16√3/3=х+4√3/3; х=12√3/3=4√3- большее основние, тогда боковая сторона треугольника, лежащая против большей стороны, равна 4√3*cos30°=(4√3/3)*√3/2=2
Треугольник, полученный в результате пересечения боковых сторон, подобен трегольнику, со сторонами - продолжением бок. сторон и меньшим основанием трапеции, по двум углам, у них угол при вершине общий, а два других соответственные при параллельных основаниях и секущей - боковой стороне. Пусть верхняя часть боковой стороны будет у, тогда справедливо соотношение 2/у=(4*3√3)/(4√3)⇒2/у=3, откуда у=2/3, тогда большая боковая сторона равна 2-2/3=1 1/3