Ход решения
Через вершину B треугольника ABC проводим фронталь и горизонталь.
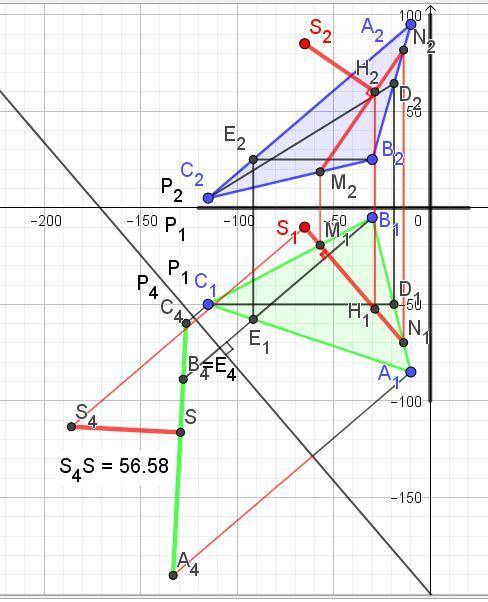
Переводим ABC в проецирующее положение. Для этого перпендикулярно В1Е1 вводим новую фронтальную плоскость Р4. Проецируем на неё точку S и треугольник ABC.
Из точки S4 проводим перпендикуляр к А4С4.
Длина отрезкаS4S – искомое расстояние между плоскостью треугольника ABC и точкой S.
Если требуется аналитическая проверка найденного расстояния, то по координатам точек А, В и С находим уравнение плоскости АВС:
95x -111y +154z - 6145 = 0.
Затем находим расстояние от точки S до плоскости АВС.
Для вычисления расстояния от точки S(Sx; Sy; Sz) до плоскости Ax + By + Cz + D = 0 используем формулу:
d = |A·Mx + B·My + C·Mz + D| /√(A² + B² + C²)
Подставим в формулу данные:
d = |95·65 + (-111)·10 + 154·85 + (-6145)| √(95² + (-111)² + 154²) = |6175 - 1110 + 13090 - 6145| /√(9025 + 12321 + 23716) =
= 12010 /√45062 = 6005√45062 /22531 ≈ 56.57672.
Полученное расчётное значение полностью совпадает с графическим расчётом.
Контрольна робота з геометрії 8 класу з теми «Подібність трикутників» містить два варіанти по 7 завдань в кожному, 4 з яких – тестові, 3 – вимагають повного розв’язання і обгрунтування
Варіант 1
(3б.) Заповніть пропуски:
а) Якщо ∆ABC ∆MNK, то B = …, M = …, C = …;
б) якщо ∆ABC ∆MNK, то ;
в) Якщо BD — бісектриса кута ABC (рис. 1), то .
У завданнях 2—4 виберіть правильну відповідь. (Кожне завдання оцінюється 1 б.)
∆АВС ∆А1В1С1, АС = 8 см, А1В1 =12 см, В1С1 =14 см, А1С1= 16 см. Знайдіть сторони АВ і ВС.
а) 24 см, 28 см; б) 6 см, 7 см; в) 14 см, 16 см.
∆АВС ∆А1В1С1, АВ = 7 см, ВС = 6 см, АС = 5 см. Знайдіть периметр трикутника A1B1C1, якщо В1С1 = 2 см.
а) 6 см; б) 24 см; в) 36 см.
Катет прямокутного трикутника дорівнює 10 см, а його проекція на гіпотенузу — 8 см. Знайдіть гіпотенузу цього трикутника,
а) 1,25 см; б) 6 см; в) 12,5 см.
Розв’яжіть задачі 5—7 з повним поясненням.
(1 б.) За даними рис. 2 доведіть подібність трикутників ABE і CDE.
(2 б.) Дві сторони трикутника дорівнюють 6 см і 8 см. Бісектриса трикутника, що проведена до третьої сторони, поділяє її на відрізки, більший з яких дорівнює 4 см. Знайдіть периметр трикутника.
(3 б.) В трапеції ABCD її основи AB і CD дорівнюють відповідно 9 см і 12 см, а одна з діагоналей дорівнює 14 см. На які відрізки ділиться ця діагональ точкою перетину діагоналей?