50 квадратных сантиметров
Объяснение:
Формула площади для трапеции:
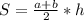 , где a и b - основания трапеции, а h - высота.
, где a и b - основания трапеции, а h - высота.
Для начала найдём сумму двух оснований. Если в трапецию можно вписать окружность, то сумма боковых сторон равна сумме её оснований. Тогда сумма оснований равна 10+10=20 (см).
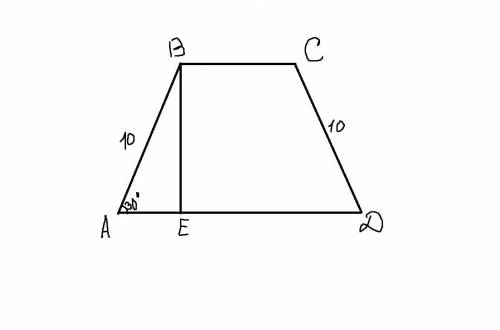
Теперь осталось найти высоту. Для начала проведём её на рисунке (BE ⊥ AD). Найдём высоту из прямоугольного треугольника ABE(∠BEA = 90°). У этого треугольника ∠BAE = 30°. Катет, лежащий напротив угла 30 градусов равен половине гипотенузы, тогда AB=2BE => 10=2BE => BE = 5 см.
Теперь, когда нам известна сумма оснований и высота, мы можем подставить все данные в формулу для нахождения площади трапеции:
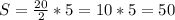 (см^2).
(см^2).
Объяснение:
Дано:
Трапеция АВСD
прямая FG
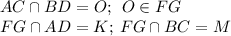
Доказать что
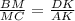
Доказательство
АВСD - трапеция => ВС || АD
Тогда диагонали АС, ВD и прямую FG можно рассматривать как секущие при 2х параллельных.
Соответственно,
- будут равны углы (как накрест лежащие):
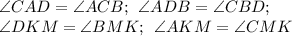
- будут равны как вертикальные:
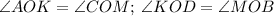
Рассм. подобные ∆-ки.
Вследствие равенства углов подобны:
∆АОК и ∆СОМ
∆DОК и ∆BОМ.
Коэффициент подобия:
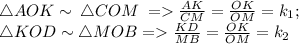
Oчевидно, что в обоих случаях коэффициент подобия можно выразить через одно и то же соотношение, а значит коэффициенты равны:
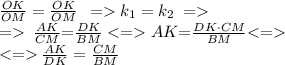
Что и требовалось доказать
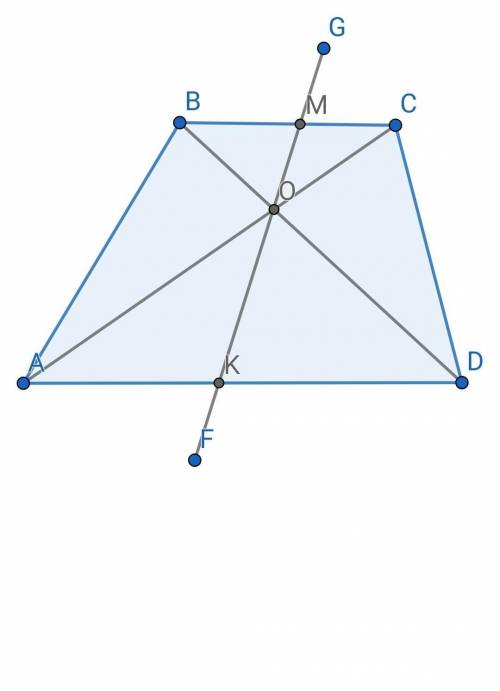
Сделаем рисунок трапеции.
Проведем из вершины С прямую СК, параллельную ВА, и высоту h.
AK=BC=10
KD=AD-BC=50-10=40
Найдем высоту h из треугольников КСМ и СМD и приравняем её значения.
h²=KC²-KM²
h²=CD²-MD²
Пусть КМ=х, тогда MD=40-х
13² - х²=37² - (40 - х)
169 - х²=1369 - 1600 + 80 - х²
80 х=400
х=5
h²=169-25=144
h=12
S трапеции = 12∙ (50+10) : 2=360 см²