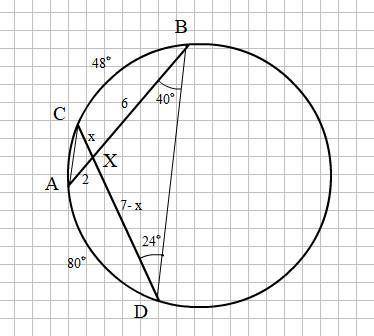
а) СХ = 1,75 см; XD = 5,25 см;
б) ∠АХС = 116°
Объяснение:
Смотри прикреплённый рисунок.
а)
∠САВ = ∠СDB = 24° так как опираются на одну и ту же дугу ВС = 48°
∠АСD = ∠ABD = 40° так как опираются на одну и ту же дугу AD = 80°
ΔACX ~ ΔDBX по двум равным углам.
Пусть СХ = x, тогда XD = 7 - x
Следовательно, AX : XB = CX : XD
2 : 6 = x : (7 - x)
2( 7 - x) = 6x
14 - 2x = 6x
8x = 14
x = 1.75 (см) - это CX
7 - x = 7 - 1.75 = 5.25 (cм) - это XD
б)
В Δ САХ известны два угла
∠САХ = ∠САВ = 24°; ∠АСХ = ∠АСD = 40°
Согласно свойству углов треугольника
∠АХС = 180 ° - (∠САХ + ∠АСХ) = 180° - (24° + 40°) = 116°
В основании правильной 4-х угольной пирамиды SABCD лежит квадрат. BSD-сечение, S=90 градусов, тогда углы В и С равны по 45 градусов, следовательно треуг. BSD-равнобедренный, BS=SD. Для вычисления объема нам нужна высота пирамиды SO, которая является также высотой треуг. BSD. Эта высота разделила треуг. BSD на два равные равнобедренные треугольника BOS и DOS, у которых OB=OD=OS. Пусть ОВ=х, тогда и OS=x, следовательно, площадь сечения:
24=х*х
x^2=24
x=√24см, OB=OD=OS=√24см
Найдем сторону основания: АВ=√(ОВ^2+AO^2)=√(24+24)=√48см, тогда площадь основания S=AB^2=48см^2
Объем пирамиды вычисляется по формуле: V=(1/3)*S*h
h=OS=√24см
V=1/3*√24*48=16√24=32√6см^3