Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
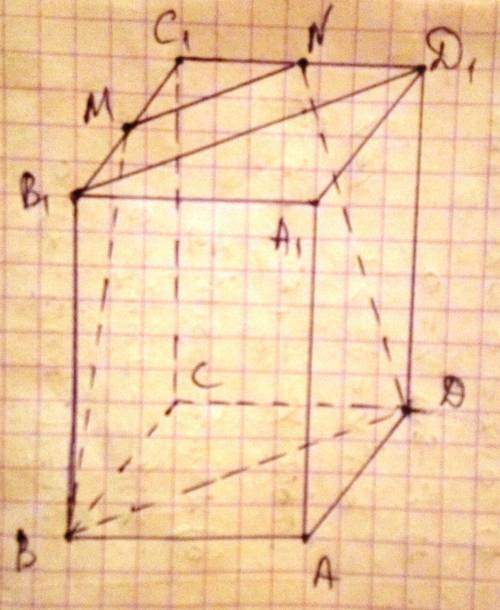
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
Объяснение:
(рис.1)
Построим график параболы, используя направление ветвей, вершину, фокус и ось симметрии.
Направление: направлено вверх
Вершина:
(1,−2)
Фокус:
(1,−23/12).
Ось симметрии:
x=1
Направляющая:
y=−25/12
x −1 0 1 2 3
y 10 1 −2 1 10
(рис.2)
Построим график параболы, используя направление ветвей, вершину, фокус и ось симметрии.
Направление: направлено вниз
Вершина:
( 2 , 5 )
Фокус:
( 2 , 39 /8 ) .
Ось симметрии:
x = 2
Направляющая:
y = 41 /8
x 0 1 2 3 4
y − 3 3 5 3 − 3