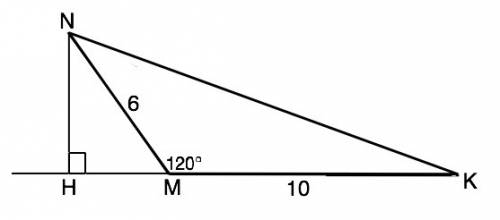
Проведем высоту из вершины N. Для тупоугольного треугольника высота из вершины острого угла пройдет вне его и пересечет продолжение стороны, в данном случае стороны МК в точке Н. В треугольнике NHM угол NMH=180°-120°=60° ( как смежный углу NMK). Тогда НМ=MN•cos60°=3 см, а катет NH=NM•sin60°=3√3 см. НК=НМ+МК=3+10=13 см. По т.Пифагора NK=√(NH²+HM²)=√196=14 см. Найдем угол К=NH:НК=3√3:14=arcsin 0,3712, что соответствует углу 21,786° или 21°47’. Из суммы углов треугольника угол N=180°=(120°+21°47´)=38°13´
———————
Эту задачу можно также решить с применением т.косинусов и затем т.синусов.
1 130 и 50 : ну постройте вы чертеж - и все увидите. проведите радиусы в точки касания, там получаются 4угольники, 2 угла прямые, значит сумма 2 других 180, один 50, другой 130, а это центральный угол дуги. Со вторым так же
2 Это египетский треугольник подобный 5,12,13. Прямой вписанный угол всегда опирается на диаметр (это - заклинание, надо выучить :)) Значит треугольнки прямоугольный, гипотенуза 26, поэтому катеты 10 и 24. Проверьте по теореме Пифагора :))) Можно и уравнение составить (типа x^2 + (x*5/12)^2 = 26^2) и вычислить, но так - веселее. :))