Проводим высоты в треугольниках АК и ДК, они соединятся о дной точке К, ВС - основание одно для двух. ВК = ВС, в равнобедренном треугольнике высота=медиане, биссектрисе
ДК = корень (ВД в квадрате - ВК в квадрате )= корень (676-576) =10
АК = корень (АВ в квадрате - ВК в квадрате )= корень ( 900- 576) = 18
В треугольнике АКД угол АКД находим по теореме косинусов
АД в квадрате = ДК в квадрате + АК в квадрате - 2 х АК х ДК х cos угла АКД
(2 х корень61)в квадрате = 10 в квадрате + 18 в квадрате - 2 х 10 х 18 х cos угла АКД
244 = 100 + 324 -360 х cos угла АКД
cos угла АКД = 180/360=1/2, что соответствует углу 60 град.
На рисунке изображен график линейной функции. Напишите формулу, которая задает линейную функцию
. Уравнение прямой в отрезках
Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид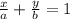
где a и b - некоторые отличные от нуля действительные числа , при чем | a| и |b| равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy, считая от начала координат.
. Через координаты 2-х точек.
Уравнение прямой у=кх+в.
Точка пересечения с Оу имеет координаты ( 0; 4)⇒ 4= к*0+в ,в=4
Точка пересечения с Ох имеет координаты (-4; 0) ⇒ 0=к*(-4)+в или
0=-4к+4 , к=1.
Уравнение прямой у=х+4.