если взять вот такой вот чертеж ( по мне так это единственный с которым можно решить ) , то нужно сделать следующее . во первых надо помнить что все стороны ромба между собой равны то есть AB=BC=CD=AD , так вот беря во внимания что угол ABC=60° и зная что диагональ ромба является еще и биссектрисой углов о есть уголы BAC и ACB между собой равны и тут получается что если в треугольника ABC эти два угла равны а третий 60° это значит треугольник является равносторонним т.к все углы его равны между собой (60°) .
А зная что AC=10 делаем вывод что все остольные стороны тоже по 10 см
а периметр 40 см
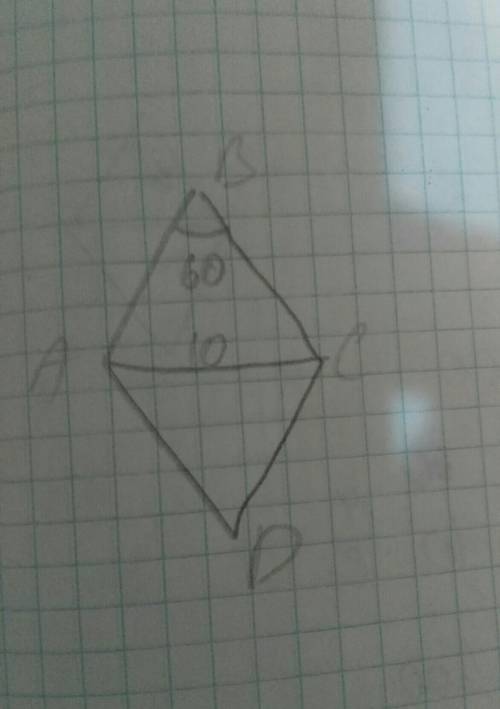
3) Р=40 ед
4) Р=22 ед
Объяснение:
3) если опустить ⊥ ВМ из вершины В на сторону АД получим прямоугольный ΔАВМ, ВМ- противолежащий катет, АВ - гипотенуза, ∠А=30
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе
тогда 5/АВ=sin30
5/AB=1/2
AB=10
Так как в ромбе все стороны равны АВ*4=40 - это и будет искомый периметр
4) мы знаем по условию что АВ+ВС+СД+АД=32 ед
Нам нужно найти АВ+ВЕ+АЕ
так как СД=ВЕ, ВС=5 и АД=АЕ+5, то можем записать
АВ+5+ВЕ+АЕ+5=32 ед
АВ+ВЕ+АЕ=22 ед