
Задача №11
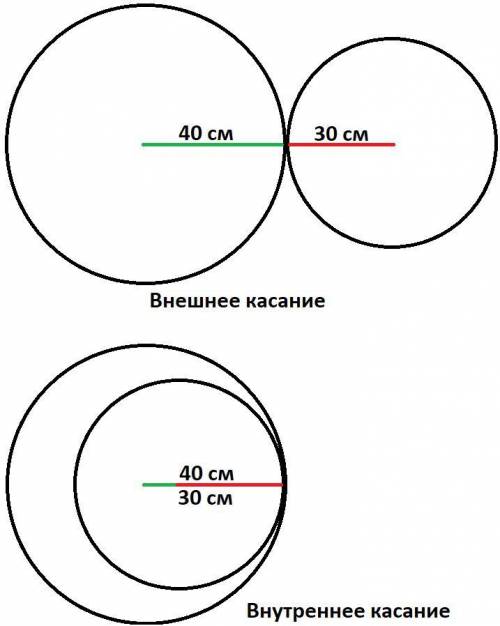
При внешнем касании расстояние между центрами будет равно сумме радиусов: 40 см + 30 см = 70 см.
При внутреннем касании расстояние между центрами будет равно разнице радиусов: 40 см - 30 см = 10 см.
ответ: при внешнем касании 70 см, при внутреннем касании 10 см.
Задача №12
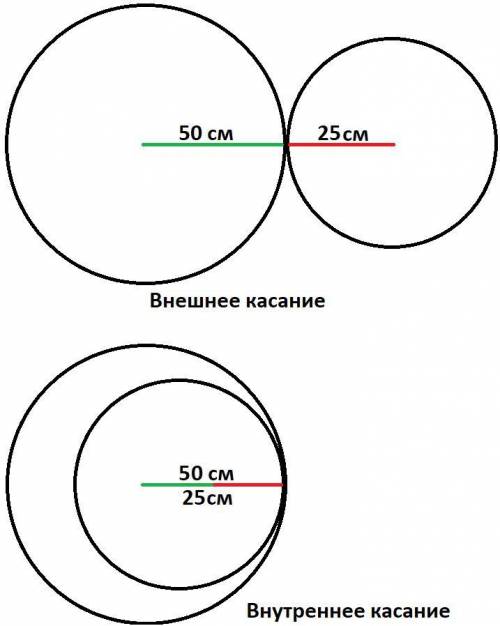
При внешнем касании расстояние между центрами будет равно сумме радиусов: 50 см + 25 см = 75 см.
При внутреннем касании расстояние между центрами будет равно разнице радиусов: 50 см - 25 см = 25 см.
Для внутреннего касания расстояние между центрами слишком большое, а для внешнего касания слишком короткое (не хватает 15 см).
Вывод: окружности с данными параметрами касаться не могут.
Продлим сторону СД до пересечения с прямой АВ в точке М.
Из вершины С трапеции опустим высоту СН на основание АД. АН=ВС=3
НД=АД-3=1
Рассмотрим треугольники МВС и СНД
∠ВСМ=∠НДС как соответственные при пересечении параллельных прямых секущей.
Следовательно, треугольники ВМС и СНД подобны по двум равным углам - прямому и острому.
Из подобия треугольников следует ∠ ВМС=∠ НСД
ВС:НД=3:1
МС:СД=3:1
МС=3 СД
Обозначим величину СД =х
Тогда МС=3х, а МД=4х
МЕ - касательная к окружности. МД = секущая
Квадрат касательной равен произведению секущей на её внешнюю часть.
МЕ²=МД*МС
МЕ²=4х*3х=12х²
МЕ=2х√3
Расстояние от точки до прямой измеряется перпендикуляром.
ЕТ ⊥ МД
Из прямоугольного треугольника МКЕ выразим ЕТ
ЕТ=МЕ*sin ВМС.
∠ВМС=∠ НСД ( из подобия треугольников)
sin∠ВМС=sin∠НСД=НД:СД=1:х ⇒
ЕТ=2х√3*1/х=2√3