ответ: 20 см
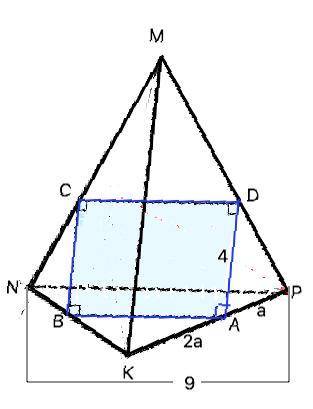
Объяснение: Рассмотрим основание NPK данного тетраэдра. Сторона АВ получившегося прямоугольника параллельна стороне PN треугольника NPK. Треугольники КВА и КNP подобны по двум углам: угол К общий, углы КАВ и КРN равны как соответственные при пересечении параллельных АВ и PN секущей КР.
Из данного в условии отношения отрезков ребра РК примем РА=а, АК=2а, ⇒ РК=РА+АК=а+2а=3а. Коэффициент подобия РК:АК=3:2 . ⇒ PN:АВ=3:2, откуда АВ=2/3 PN=9•2/3=6 дм.
Противоположные стороны прямоугольника равны. Р(АВСD)=2•(АВ+АD)=2•(6+4)=20 (см)
OA=OB=OC (радиусы окружности)
OA=OB=OC=BA=BC => △BAO, △BCO равносторонние => ∠ABO=∠OBC=60 (в равностороннем треугольнике все углы равны 60)
∠ABC=∠ABO+∠OBC=120
∠ADC=180-∠ABC=60 (сумма противолежащих углов вписанного четырехугольника равна 180)
∠BAD=∠DCB=90 (вписанные углы, опирающиеся на диаметр)
2) BH=9; AC=24
AB=BC
AH=AC/2 (в равнобедренном треугольнике высота является медианой)
AB=√(AH^2+BH^2) = √(24^2/4 +9^2) =15
Центр вписанной в треугольник окружности - точка пересечения биссектрис.
Биссектрисы треугольника делятся точкой пересечения в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
BO/OH =(AB+BC)/AC = 2AB/AC =30/24 =5/4
r= OH = BH*4/9 =4
R= AB*BC*AC/2*S = AB*BC/2*BH = 15^2/2*9 =12,5
Проверка:
r*R= AB*BC*AC/2(AB+BC+AC)
15*15*24/2(15+15+24) = 50 = 4*12,5