Периметр равностороннего треугольника равен 24 (единиц измерения)
Объяснение:
Дано: △ABC - равносторонний. BD - медиана.BD=4√3
Найти: Периметр △ ABC
В равностороннем треугольнике все стороны равны. Обозначим сторону треугольника а.
Тогда AB=BC=CD=а.
Так как медиана треугольника делит сторону пополам, то AD=DC= a/2.
Медиана равнобедренного треугольника (а равносторонний треугольник - частный случай равнобедренного) является также высотой, следовательно BD⟂AC.
Рассмотрим прямоугольный треугольник BCD.
По теореме Пифагора:
BD²+DC²=BC²
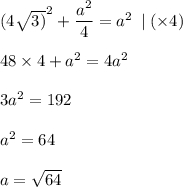
a=8 (ед)
Таким образом, сторона равностороннего треугольника равна 8.
Периметр треугольника- это сумма всех его сторон. Значит:
Р(ABC)=3•a=3•8=24(ед)
4) А и Б
5) В
6) А-3; Б-1; В-2
Объяснение:
4) подходит А и Б, так как оба этих графика пересекают ось у в положительном значении у( выше оси Х)
5) подходит В, так как пересекает ось у в отрицательном значении у( ниже оси Х)
6) а-3, так как график параллелен оси Х, значит коэффициент к=0, коэффициент b>0, так как пересекает ось у в положительном значении у (выше оси Х)
б-1, так как функция убывает, а значит коэффициент к<0, коэффициент b> 0 так как график функции пересекает ось у в положительном значении у (выше оси Х)
в-2, так как функции возрастает, значит коэффициент к>0, коэффициент b<0, так как график функции пересекает ось у в отрицательном значении у (ниже оси Х)