ответ: 80.
Объяснение:
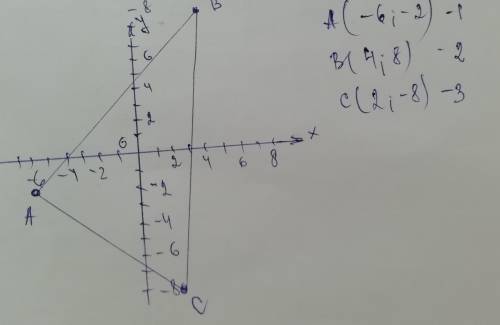
Построим координатную плоскость и нанесем точки А,В,С. (смотри чертёж).
Чтобы найти площадь при таких данных, воспользуемся формулой Герона:
S = √p(p-a)(p-b)(p-c), где a, b и c - стороны треугольника р=(a+b+c)/2 - полупериметр треугольника.
Но есть более простая формула:
S=1/2|(x2-x1)(y3-y1)-(x3-x1)(y2-y1|); (| | - по модулю);
Обозначим точки 1 - А; 2 - В; 3 - С.
Тогда S= 1/2| (4-(-6))(-8-2)-(2-(-6))(8-(-2))|=1/2| (10*(-6))-(10*10)|=1/2| (-60-100) |= 1/2 |-160|=1/2* 160=80.
30 см
Объяснение:
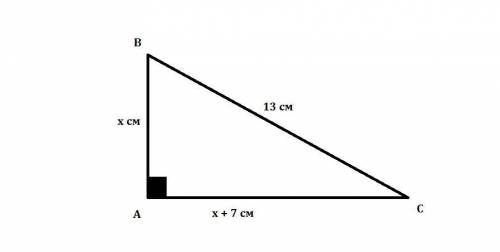
Рассмотрим вложение.
Нам дан ΔАВС: ∠А = 90°, ВС = 13 см
Пусть АВ = х см, тогда АС = х + 7 см. Воспользуемся т.Пифагора для нахождения стороны.
АВ² + АС² = ВС²
х² + (х + 7)² = 13²
х² + х² + 14х + 49 = 169
2х² + 14х + 49 - 169 = 0
2х² + 14х - 120 = 0 |:2
х² + 7х - 60 = 0
D = 7² - 4 * (-60) = 49 + 240 = 289 = 17²
x₁ = (-7 - 17)/2 = -24/2 = -12
x₂ = (-7 + 17)/2 = 10/2 = 5
т.к. сторона не может быть отрицательна, то АВ = 5 см, тогда
АС = 5 + 7 = 12 см
Чтобы найти периметр треугольника, надо сложить все стороны.
Р = АВ + ВС + АС = 5 + 13 + 12 = 30 см
допустим тут написано что то умное