1. По Пифагору квадрат второго катета равен 36²-12²=(36-12)*(36+12)=24*48
И этот же квадрат катета равен произведению гипотенузы на искомую проекцию этого катета на гипотенузу, поэтому проекция равна 48*24/36=8*24/6=8*4=32/см/
2. Площадь треугольника АВС равна половине произведения АВ и АС на синус 45°, т.е. 5√2*8*(√2/2)/2=20
средними линиями мы разбиваем треугольник на четыре равных, а значит, и равновеликих, т.е. с равными площадями. поэтому искомая площадь 20/4=5/см²/
4. формулы параллельного переноса
х'=x+a
y'=y+b
0=3+a⇒a=-3
6=2+b⇒b=4
Пусть С(х;у)
х+а=-3
у+b=2, подставим а и b для точек С и D, получим
х+(-3)=-3⇒х=0
у=-4+2=-2
D(0; -2)
Объяснение:
1
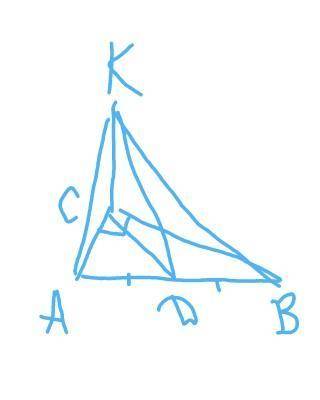
Рассмотрим тр-к АВС
По теореме Пифагора :
АВ=корень (АС^2+ВС^2)=
=корень (24^2+32^2)=корень 1600=40 мм
СD=AD=BD=AB:2=40:2=20 мм
Тр-к КСD:
По теореме Пифагора :
КD=корень (КС^2+СD^2)=
=корень (48^2+20^2)=корень 2704=
=52 мм
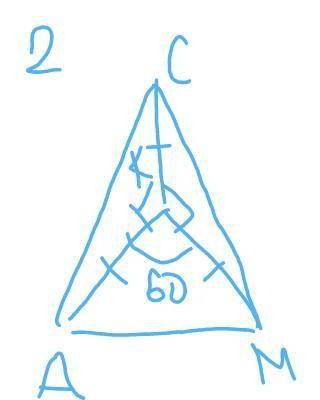
2
А) АК _|_ МК - НЕТ (т. к <МКА=60 градусов)
Б) тр-к АКС - прямоугольный - ДА(т. к <АКС=90 градусов)
В) тр-к МАК - равносторонний - ДА (т. к
КА=КМ, значит тр-к АКМ-равнобедренный, т. к <МКА=60 градусов <КАМ=<КМА=(180-<МКА)/2=
=(180-60)/2=60 градусов, значит тр-к
МАК- равносторонний
Г) МК_|_(АКС) - ДА
Д) тр-к МАС - прямоугольный - НЕТ
ответ : Б) ; В) ; Г)
Каждая точка на прямой разбивает эту прямую на две части так, что точки из разных частей лежат по разные стороны от данной точки, а точки из одной части лежат по одну сторону от данной точки.
Лучам, или полупрямой, называется часть прямой, состоящая из данной точки и всех точек, лежащих от неё по одну сторону. При этом сама данная точка называется вершиной луча, или началом.
Для обозначения лучей используются строчные латинские буквы, например, а, или пары прописных латинских букв, например АВ, первая из которых обозначает начало луча, а вторая - какую- нибудь точку, принадлежащую лучу
Объяснение:
Отрезком называется часть прямой, состоящая из двух данных точек и всех точек, лежащих между ними. При этом сами данные точки называются концами отрезка.
Отрезок обозначается указанием его концов. Например, АВ, C1D1
всегда