Даны два равных треугольника: ΔABC и ΔA1B1C1. Стороны треугольников относятся как AB : BC : AC = A1B1 : B1C1 : A1C1 = 5:7:11, а сумма наибольшей и наименьшей сторон треугольника A1B1C1 равна 80 см. Выбери правильные ответы.
Длина стороны AB –
.
Длина стороны A1C1 –
.
Периметр ΔA1B1C1 –
.
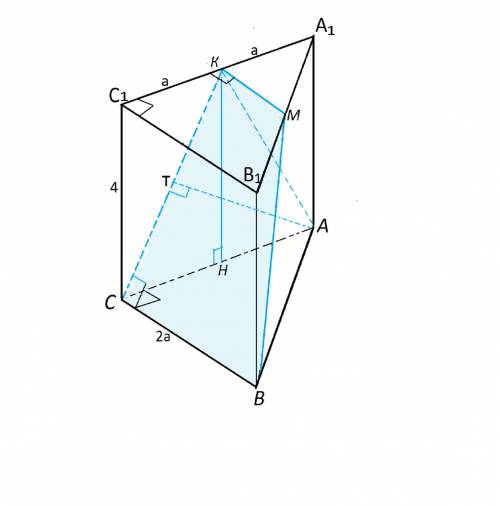
В прямой призме в основании лежит прямоугольный равнобедренный треугольник. Найти площадь сечения, проходящего через катет нижнего основания и середину гипотенузы верхнего, если расстояние между основаниями 4 и равно расстоянию от вершины нижнего основания до плоскости сечения.
Сделаем рисунок призмы.
Сечение пересекает верхнее основание призмы по прямой КМ, параллельной СВ и, следовательно, параллельной С₁В₁.
Так как К - середина катета С₁А₁, прямая КМ - средняя линия треугольника А₁С₁В₁.
С₁К=КА₁
Опустим на АС перпендикуляр КН. Он равен высоте призмы. Прямоугольники СС₁КН и АА₁КН равны, т.к. имеют равные стороны.
⇒ их диагонали СК и АК также равны.
⇒ Треугольник СКА - равнобедренный с высотой КН.
АТ - также является высотой этого равнобедренного треугольника, проведенной к его боковой стороне КС ( расстояние от точки до плоскости есть перпендикуляр ) и по условию равна высоте призмы.
⇒ КН=АТ=4
Если высоты равнобедренного треугольника, проведенные к основанию и боковой стороне, равны, этот треугольник - равносторонний и все углы в нем равны 60°
АС=СВ=АК=СК
АС=СВ=КН:sin (60°)=8:√3
КМ=СВ:2=4:√3 СК=АС=8:√3 и перпендикулярна СВ ( по теореме о трех перпендикулярах)
СКМВ - прямоугольная трапеция. Площадь трапеции равна произведению высоты (КС) на полусумму оснований.
(КМ+СВ)=8:√3 + 4:√3 =12:√3 =4√3
S (СКМВ)=(8:√3)*(4 √3):2=16 единиц площади)
----------
[email protected]