а) По определению проекция фигуры на плоскость - совокупность проекций всех точек этой фигуры на плоскость проекции.
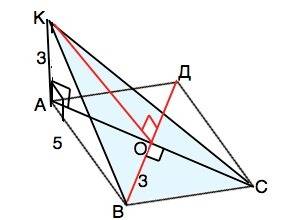
Точка К проецируется в основание перпендикуляра КА, т.е. в т. А.
Т. В и С ∆ КВС лежат в плоскости ромба. Через две точки можно провести только одну прямую. ⇒
Все точки сторон ∆ КВС проецируются на стороны ∆ АВС. ⇒
∆ АВС проекция ∆ КВС на плоскость ромба АВCД.
б) КА перпендикулярен плоскости ромба, следовательно, перпендикулярен любой прямой, проходящей в этой плоскости через т. А. ⇒КА⊥АС
Диагонали ромба взаимно перпендикулярны.⇒АС⊥ВД
АО - высота равнобедренного ∆ АВД. Из ∆ АОВ по т.Пифагора АО=√(B²-BO²)=√(25-9)=4
Расстояние от точки до прямой равно длине проведенного между ними перпендикуляра.
КО по т. о 3-х перпендикулярах перпендикулярен ВД.
Из прямоугольного ∆ КАО расстояние КО=√(КА²+АО*)=√(9+16)=5 см
площадь трапеции
площадь трапеции равна произведению полусуммы ее оснований на высоту:
s = ((ad + bc) / 2) · bh,
где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
доказательство.

рассмотрим трапецию abcd с основаниями ad и bc, высотой bh и площадью s.
докажем, что s = ((ad + bc) / 2) · bh.
диагональ bd разделяет трапецию на два треугольника abd и bcd, поэтому s = sabd + sbcd. примем отрезки ad и bh за основание и высоту треугольника abd, а отрезки bcи dh1 за основание и высоту треугольника bcd. тогда
sabc = ad · bh / 2, sbcd = bc · dh1.
так как dh1 = bh, то sbcd = bc · bh / 2.
таким образом,
s = ad · bh / 2 + bc · bh = ((ad + bc) / 2) · bh.это можно только с доказательством
Висота ділить основу на дві частини 24/2=12см.Розглянемо один із двох менших трикутників.Дано катет 12 см і гіпотенузу 13 см.За теоремою Піфагора знайдемо другий катет(висоту).
13*2=12*2+х*2
169=144+х*2
х*2=25
х=5см