Объяснение:
Я вспомнил, что у данной задачи есть три решения. Сейчас поясню их всех.
Дано: на отрезке АС лежит два отрезка-АВ и ВС.
Найти: ВС
Решение: АС=АВ+ВС ВС=АС-АВ ВС=47-19=28 см.
ответ. 28 см.
Дано: на отрезке ВС лежит два отрезка-ВА и АС
Найти: ВС
Решение: ВС=АВ+АС ВС=47+19=66 см.
ответ. 66 см.
Дано: на отрезке АВ лежит два отрезка-АС и СВ
Найти: ВС
Решение: АВ=АС+ВС ВС=АВ-АС ВС=19-47=-28
Так как ответ отрицательный то в данном случае ответа нет.
Надеюсь я всё пояснил.
P.S. Можно лучший ответ. :)
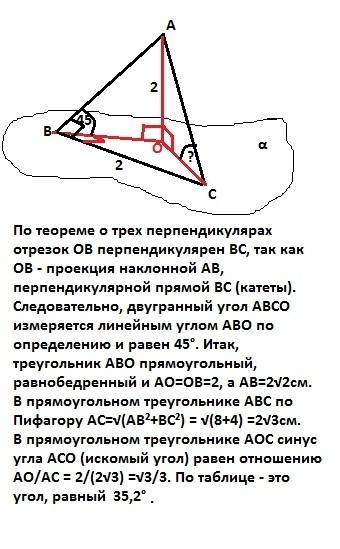
По теореме о трех перпендикулярах отрезок ОВ - проекция наклонной АВ, перпендикулярной прямой ВС (катеты). Следовательно, двугранный угол АВСО измеряется линейным углом АВО по определению и равен 45° (дано). Треугольник АВО прямоугольный и равнобедренный. Катеты АО=ОВ=2см, а гипотенуза АВ=2√2 см. В прямоугольном треугольнике АВС по Пифагору АС=√(АВ² +ВС²) = √(8+4) = 2√3см. В прямоугольном треугольнике АОС синус угла АСО (искомый угол, так как это угол между наклонной АС и плоскостью α по определению) равен отношению АО/АС = 2/(2√3) = √3/3. По таблице - это угол, равный 35,2°.
ответ: 35,2°.
По теореме о трех перпендикулярах отрезок ОВ - проекция наклонной АВ, перпендикулярной прямой ВС (катеты). Следовательно, двугранный угол АВСО измеряется линейным углом АВО по определению и равен 45° (дано). Треугольник АВО прямоугольный и равнобедренный. Катеты АО=ОВ=2см, а гипотенуза АВ=2√2 см. В прямоугольном треугольнике АВС по Пифагору АС=√(АВ² +ВС²) = √(8+4) = 2√3см. В прямоугольном треугольнике АОС синус угла АСО (искомый угол, так как это угол между наклонной АС и плоскостью α по определению) равен отношению АО/АС = 2/(2√3) = √3/3. По таблице - это угол, равный 35,2°.
ответ: 35,2°.

ответ указан на изображении.