Изобразите остроугольный треугольник авс, где ав вс. постройте при циркуля и линейки точку пересечения - id138689820210314 от LaGGeRiSTiK 14.03.2021 18:45

Question

Геометрия: Изобразите остроугольный треугольник авс, где ав вс. постройте при циркуля и линейки точку пересечения высоты вн и медианы вм этого трекгольника.

LaGGeRiSTiK · Accepted Answer

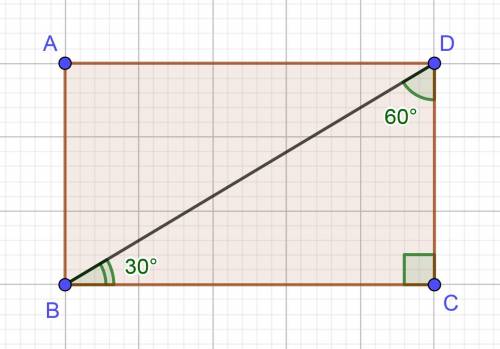
Нехай дано прямокутник ABCD, BD — діагональ, DC = 10 см, ∠BDC = 60°.

Р-мо BDC:

∠BCD = 90° — як кут прямокутника, отже ΔBDC — прямий, ∠BDC = 60° — за умовою, тоді ∠DBC за теоремою про суму кутів трикутника буде дорівнювати:

∠DBC = 180°−90°−60° = 30°.

По властивості катета, який лежить напроти кута 30°, гіпотенуза трикутника буде рівна:

BD = 2*DC = 2*10 = 20 (cm)

Знайдемо інший катет за т. Піфагора:

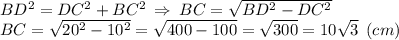
$BD^2=DC^2+BC^2 \:\Rightarrow\: BC = \sqrt{BD^2-DC^2} \\BC = \sqrt{20^2-10^2} = \sqrt{400-100} = \sqrt{300} = 10\sqrt{3} \:\: (cm)$

Підставимо значення у формулу площі прямокутника:

$S = DC\cdot BC\\S = 10\sqrt{3} \cdot 10 = 100\sqrt{3} \approx 173,2\:\: (cm^2)$

Відповідь: Площа прямокутника рівна 100√3 см² або приблизно 173,2 см².

Сторона прямокутника 10 см і утворює з діагоналлю кут 60 градусів . Знайдіть площу прямокутника.

Изобразите остроугольный треугольник авс, где ав < вс. постройте при циркуля и линейки точку пересечения высоты вн и медианы вм этого трекгольника.

MOGZ ответил