13. Знайдіть cosa i tgа, якщо ѕіn a = 0,6 і кут а тупий

Question

Геометрия: 13. Знайдіть cosa i tgа, якщо ѕіn a = 0,6 і кут а тупий​

Sjsjssj · Accepted Answer

Так как многоугольник - правильный, то все стороны и углы у этого многоугольника равны.

Сначала найдём количество сторон этого многоугольника.

Итак, угол правильного многоугольника вычисляется по формуле :

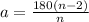
$a=\frac{180(n-2)}{n}$

Где a - угол правильного многоугольника, n - количество сторон.

Подставим известные значения в формулу и узнаем численное значение переменной n :

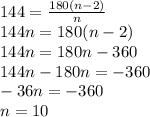
$144=\frac{180(n-2)}{n}\\144n = 180(n-2)\\144n = 180n-360\\144n-180n = -360 \\-36n = -360\\n = 10$

Количество сторон = 10.

2) Периметр многоугольника - сумма длин всех сторон.

Можно записать формулу для нахождения периметра правильного многоугольника так :

P=n*d

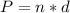
Где P - периметр, n - количество сторон, d - длина стороны.

Нам нужно найти d :

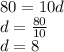
$80=10d\\d=\frac{80}{10} \\d = 8$

Сторона многоугольника = 8 см.

ответ: 8 см.

13. Знайдіть cosa i tgа, якщо ѕіn a = 0,6 і кут а тупий​