Дано:
<Е=30°
<С=90°
СР-?
Катет, лежащий напротив угла 30°, равен половине гипотенузы:
CP=PE/2
CP=46/2
CP=23м
ответ: СР=23м
Дано :
∆АВС — равнобедренный (АС — основание).
АВ = ВС = 5√3.
<С = 30°.
СН — высота.
Найти :
СН = ?
В равнобедренном треугольнике углы при основании равны.Следовательно —
<А = <С = 30°.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.То есть —
Внешний <В = <А + <С
Внешний <В = 30° + 30°
Внешний <В = 60°.
Рассмотрим прямоугольный ∆ВСН (СН лежит вне треугольника, так как ∆АВС — тупоугольный).
BC — гипотенуза (так как лежит против угла в 90°).
Тогда —
Sin(<HBC) = CH/BC (по определению синуса острого угла прямоугольного треугольника)
Sin(60°) = CH/(5√3)
Обозначим СН за х.
Тогда —
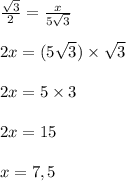
СН = 7,5 (ед).
7,5 (ед).
— — —
Надеюсь, я Вам. Есть вопросы по поводу решения? Задавайте в комментариях.
1. 1) ∠AOD=∠BOC=130° (вертикальные), значит ∪ ВС=130°(стягивает центральный угол).
2)∪ АВ=∪АС- ∪ВС=180°-130°=50°, значит
∠АСВ =50/2=25 °(вписанный не центральный угол)
2. 1) ∆ АВС- равнобедренный , значит ∠ А=∠С=(180°-177°)/2=1,5°.
2) ∪ ВС=1,5°·2=3° (стягивает вписанный угол), тогда ∠ВОС=3° (центральный угол )
3. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-7°=83° .
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=83°.
4. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-84°=6°
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=6°.
5. ∠ ABC =90°(вписанный), т.к ∪ АС=180° (опирается на диаметр АС). Тогда ∠С=180°-90°-75°=25°
6. 1) ∪ AN=73°·2=146° (стягивает вписанный ∠ NBA). Тогда
∪ NB =∪ AB-∪AN=180°-146°=34°.
2) ∠NMB=34°/2=17° (вписанный не центральный угол)
7. 1) ∆ АОВ- равнобедренный(АО=ОВ=r), значит ∠ОАВ=∠АВО=15°. Тогда ∠ОВС =56°-15°=41°.
2) ∆ ВОС- равнобедренный(ВО=ОС=r), значит ∠ОВС=∠ВСО=41°.
8. ∆ АОВ =∆ СОD (AO=OD=r, CO=OB=r, ∠AОВ =∠CОD-вертикальные ), значит ∠ОАВ =∠ОСD=25°

ответ:23м
Объяснение: Искомый катет СР лежит против угла в 30°⇒ СР=РЕ/2=46/2=23/м/