
ЗАДАНИЕ 1
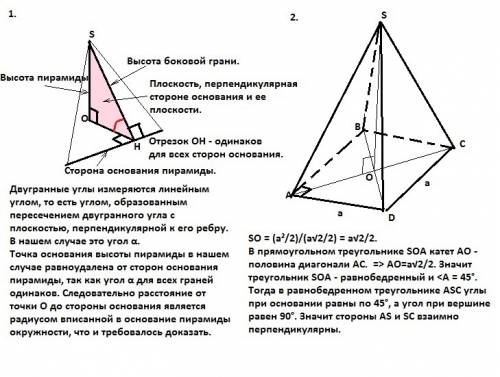
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.
Проведем через вершину пирамиды S плоскости, перпендикулярные ребрам двугранных углов пирамиды, то есть плоскости, перпендикулярные сторонам основания пирамиды и, следовательно, перпендикулярные самому основанию.
Тогда у всех этих плоскостей имеются две общие точки: вершина пирамиды S и ее проекция на основание пирамиды точка О. То есть эти плоскости пересекаются по прямой SO, являющейся высотой пирамиды. Линии пересечения этих плоскостей и пирамиды - это высота боковой грани и перпендикуляр из точки О основания высоты пирамиды к стороне основания пирамиды. Этот перпендикуляр - проекция высоты боковой грани на плоскость основания и в силу равенства двугранных углов (дано) одинаков для всех проведенных плоскостей, так как тангенс этих углов равен отношению высоты пирамиды к проекции высоты боковой грани. Итак, точка основания высоты пирамиды в нашем случае равноудалена от сторон основания пирамиды, следовательно, расстояние от этой точки до стороны основания пирамиды является радиусом вписанной в основание пирамиды окружности, что и требовалось доказать.
ЗАДАНИЕ 2.
Основание правильной пирамиды SABCD - квадрат ABCD со стороной "а". Его площадь равна а². Значит площадь диагонального сечения равна а²/2 (дано). Диагональное сечение правильной пирамиды - равнобедренный треугольник ASC с основанием - диагональю квадрата, равной а√2. Площадь диагонального сечения S=(1/2)*АС*SO (SO - высота пирамиды). Итак, (1/2)*а√2*SO = а²/2. Тогда
SO = (а²/2)/(а√2/2) = a√2/2. В прямоугольном треугольнике SOA катет АО - половина диагонали АС. АО=a√2/2. Значит треугольник SOA - равнобедренный и <A = 45°. Тогда в равнобедренном треугольнике ASC углы при основании равны по 45°, а угол при вершине равен 90°. Значит стороны AS и SC взаимно перпендикулярны.
AS и SC - противоположные ребра пирамиды. Они перпендикулярны. Что и требовалось доказать.
1.Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
АС-основание треугольника, значит МЕ=10 см.
2. Если же Ме не доказана, что она средняя линия, то сначала докажет это тождество.
Дан треугольник АВС.
Проведем прямую параллельную АС через точку М. По т. Фалеса отрезок пересекает сторону АВ в её середине.
Проведем прямую параллельную АВ из точки М. Тогда АЕМР-параллелограмм( Р-точка,которая лежит на стороне АС). У параллелограмма противоположные стороны =. Значит ЕМ=АР, АЕ=МР. Тогда ЕМ=1/2 АС. 2ЕМ=Ас. Ем=10 см.
Немного не понимаю, зачем даны другие стороны.
а || d по аксиоме: Если две прямые параллельны третьей прямой, то они параллельны => а||b||c||d