Проведем диагональ трапеции и рассмотрим образовавшиеся треугольники. Пара противоположных сторон ромба являются средними линиями этих треугольников, каждая из них параллельна этой диагонали и равна ее половине. Отсюда эта пара - равные и параллельные стороны, т.е. четырехугольник - параллелограмм. Аналогично другая пара противоположных сторон равны. А т.к.к трапеция равнобедренная, то ее диагонали равны. Значит все стороны четырехугольника равны. Таким образом, четырехугольник - параллелограмм с равными сторонами, т.е. ромб.
1. Рассмотрим треугольники, образованные соединением середин сторон треугольника. Они равны (по прямым углам и катетам). Значит гипотезы равны => у четырёхугольника все стороны равны. 2. Рассмотрим противолежащие углы образованного четырёхугольника. Они равны развёрнутому углу минус два равных угла, прилежащих к гипотенузе. Так как треугольники равны, то соответствующие углы равны, значит и противолежащие углы четырёхугольника равны. 3. Параллелограмм, у которого все стороны равны, является ромбом. Четырёхугольник, у которого противолежащие углы равны, является параллелограммом. Следовательно, четырёхугольник - ромб. Ч.т.д.
MC=2
Объяснение:
1) найти углы треугольника ABC: Пусть ∠A=x, тогда ∠B=2x, ∠C=3x. Т.к сумма углов треугольника равна 180°, ∠A+∠B+∠C=180°⇔x+2x+3x=180°⇔6x=180°⇔x=30°⇔ ∠A=30°, ∠B=60°, ∠C=90°.
2) найти углы треугольника BMC: BM биссектриса, значит ∠CBM=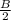
=60°:2=30°. M∈AC⇒∠BCM=∠BCA=∠C=90°.
3) найти MC: ∠BCM=90°, т.е BMC - прямоугольный треугольник. Тогда,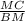
=sin∠CBM=sin30°=
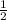⇔BM=2MC⇔MC=0,5BM=0,5×4=2