6 ед.
Объяснение:
В правильной усеченной пирамиде в основаниях лежат правильные многоугольники, стороны которых соответственно равны между собой. Боковые грани такой пирамиды - равные между собой равнобокие трапеции. Радиусы окружностей, вписанных в основания, проведенные в точки касания сторон оснований с соответственной окружностью Н и Н1, перпендикулярны к сторонам оснований по свойству радиусов, проведенных в точки касания.
Проведем перпендикуляр из точки касания Н1М верхнего основания на нижнее основание. Тогда отрезок Н1Н перпендикулярен стороне основания АВ по теореме о трех перпендикулярах, то есть является искомой высотой боковой грани.
В прямоугольном треугольнике НН1М угол ∠НН1М = 30° по сумме острых углов. Следовательно, НН1 = 2·НМ по свойству катета, лежащего против угла 30°.
НМ = ОН - О1Н1 = 8-5 = 3 ед.
Высота боковой грани НН1 = 6 ед.
1) радиус вписанной окружности равен 5
радиус описанной окружности равен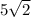
2) 4 - стороны у квадрата
Объяснение:
1) радиус вписанной окружности равен 5 см
2) это квадрат. Так как, если вписать в него окружность, то радиус этой окружности равен половине стороны квадрата.
То есть 10см (длина стороны квадрата) :2=5 см (длина радиуса вписанной окружности)
Ну у квадрата 4 стороны.
Если же это радиус описанной окружности, то он равен половине диагонали квадрата. По теореме Пифагора диагональ квадрата равна
Теперь его половина равна