(-2,2; -0,6)
Объяснение:
Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:
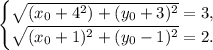
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.
Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно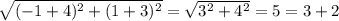 
. Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо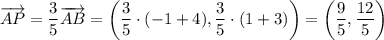 
Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор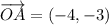 
, мы получим координаты точки P(x₀, y₀): 
.
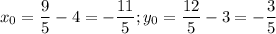Решением системы является точка (-2,2; -0,6).
Б. Житков «Про волка» (цикл рассказов)
Главная мысль произведения: приручения дикого зверя – дело сложное, требующее терпения, силы и смелости.
Рассказ «Дикий зверь»
Главная мысль: дикий зверь, даже детеныш, существо опасное, но, как и все малыши, ценящее заботу и ласку.
Главные герои: рассказчик, его мать, волчонок.
Рассказ «Как я учил волка «тубо»
Главная мысль: обучение первой команде давалось сложно, в процесс оказались вовлечены многие окружающие, их и терпение сделали свое дело.
Главные герои: рассказчик, волчонок, собака Плишка.
объём призмы равен