
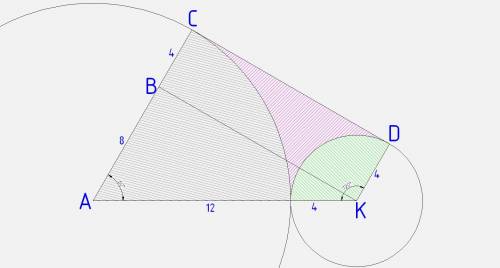
АСДК - трапеция, основания АС=12 см и ДК=4 см
АВ = 12-4 = 8 см
АК = 12+4 = 16 см
По Пифагору
ВК² = АК²-АВ² = 16²-8² = 256-64 = 3*64
ВК = 8√3 см
∠ВАК = arccos(АВ/АК) = arccos(1/2) = 60°
∠ВКА = 90 - ∠ВАК = 30°
∠ДКА = ∠ВКА + 90 = 120°
Полная площадь трапеции
S(ACDK) = 1/2(AC+DK)*BK = 1/2(12+4)*8√3 = 64√3 см²
Площадь сектора большого круга (серая штриховка)
S₁₂ = πR²/360*α = π*12²*60/360 = π*12*12/6 = 24π см²
Площадь сектора малого круга (зелёная штриховка)
S₄ = πR²/360*α = π*4²*120/360 = π*16/3 = 16π/3 см²
И площадь странной фигуры около касательной
S = S(ACDK) - S₁₂ - S₄ = 64√3 - 24π - 16π/3 см²
S = 64√3 - 88π/3 см²
bh- биссектриса
тупой угол = 150, тогда острый = 30
При проведении биссектрисы получается треугольник abh, где 2 угла будут равны по 75 градусов, т. е он равнобедренный, значит стороно ab=ah=16.
Теперь в этом трегольнике проведем высоту из угла А. Получится что она лежит против угла в 30 градусов и равна половине гипотенузы= 16:2=8
Площадь параллелограмма = 8*(16+5)=168 см^2
2)
площадь ромба равна 1/2*d*d1
где d и d1 это диагонали ромба
и получается следуещее
d/d1=3/4
4d=3d1
d=3d1/4
S=1/2*d*d1
24=1/2*3*d1/4*d1
24=3*d1^2/8
8=d1^2/8
d1^2=8*8
d1=8
d=3*d1/4=3*8/4=6
сторона ромба по теореме пифагора получится так
a^2=(d/2)^2+(d1/2)^2 где a- это сторона ромба
a^2=(d/2)^2+(d1/2)^2
a^2=(6/2)^2+(8/2)^2=9+16=25
a=5
P=4*a=4*5=20
3.
Периметр ромба равен 4*сторона
сторона равна периметр\4
сторона ромба равна 52\4=13 см
Площадь ромба равна произведению квадрата стороны на синус угла между сторонами
отсюда синус угла равен площадь робма разделить на квадрат стороны
sin A=120\(13^2)=120\169
Так как угол А -острый, то cos A=корень (1-sin^2 A)=корень (1-(120\169)^2)=
=119\169
По одной из основніх формул тригонометрии
tg A=sin A\cos A=120\169\(119\169)=120\119
ответ: 120\169,119\169,120\119.