Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
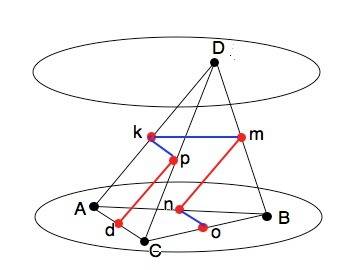
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
ответ:
ответ:
средняя линия трапеции равна полусумме её оснований. (а+б)/2=45, а+б=90(см), кусочек большего основания(между боковой стороной и высотой) найдем по т. пифагора. он равен корень из (41в квадрате - 40 в квадрате) = 9 см. таких отрезков два(и около второй боковой стороны). а-верхнее основание трапеции, б-нижнее основание, причем б=а+9+9=а+18. а+а+18=90, 2а=72, а=36, б=36+18=54. ответ: 36 см и 54 сантиметра
объяснение:
объяснение: