Можно было еще верхногами сфотать? Вообще неудобно.
1А1. В первом треугольники не разберу цифры, но т.к сумма треугольника = 180 градусов => 180-76-87=17 градусов x
1А2 Точно также = 180 - 28 - 55 = 97 градусов x
2А1 Во втором ряду используются равнобедренные треугольники, у которых углы при ОСНОВАНИИ РАВНЫ
Из этого следует y = 73 градуса, а дальше мы применяем правило = 180 - 73-73 = 34 градуса x
2А2 Точно также y = 47, = 180 - 47 - 47 = 86
3А1 Здесь нужно применить такую хитрость.
(180 - 62) : 2 = 59 градусов x и y
3А2 Точно также (180 - 84) : 2 = 48 градусов x и y
4А1 и 2 я не знаю как решать
5А1 - там внешний угол со смежной стороной, благодаря которой находим x = 180 - 108 = 72, далее находим y = 180 - 49 - 72 = 59 - y
5А2 - аналогично 180 - 98 = 82, y = 180 - 82 - 32 = 66 - y
6А без понятия...
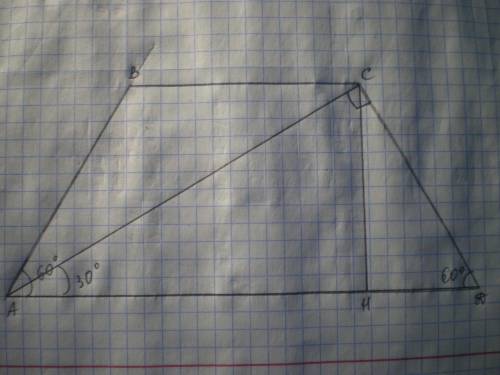
Дано: АВСД - трапеция, АВ=СД, АД=8√3, ∠А=∠Д=60°, АС⊥СД. Найти S(АВСД).
Решение: Проведем высоту СН, тогда S(АВСД)=(ВС+АД):2*СН.
Рассмотрим ΔАСД - прямоугольный, ∠Д=60°, тогда ∠САД=90-60=30°, а СД=1\2 АД=8√3:2=4√3.
Диагональ АС перпендикулярна к боковой стороне и делит угол А пополам, значит большее основание трапеции в два раза больше меньшего основания и её боковых сторон; и высота трапеции равна половине её диагонали.
СД=ВС=8√3:2=4√3;
АС²=(8√3)²-(4√3)²=192-48=144; АС=√144=12.
СН=1\2 АС=12:2=6.
S(АВСД)=(4√3+8√3):2*6=36√3 (ед²).
ответ: 36√3 ед²
Я так думаю, что такое решение будет полезно :)
Я разметил начало координат в точке, в которой пересекаются продолжения ребер (то есть в вершине НЕусеченной пирамиды) и принял за ось X прямую вдоль высоты пирамиды.
Надо построить функцию y(x), где x - расстояние от О вдоль оси X (то есть высота), а y - площадь сечения пирамиды перпендикулярной плоскостью.
В САМОМ ОБЩЕМ СЛУЧАЕ
y = a*x^2;
Ясно, что площадь пропорциональна квадрату расстояния (а если не ясно - полезно понять, почему :)), причем при x = 0 y = 0 (так выбрано начало координат).
а - неизвестная величина.
Что известно? А вот что:
1. При x = x1; y = 18;
2. При x = x2; y = 128;
3. Точка x0 выбрана так, что (x0 - x1)/(x2 - x0) = 2/3;
Найти надо y при x = x0;
Легко видеть, что (x2/x1)^2 = 128/18 = (8/3)^2; то есть x2/x1 = 8/3;
Я ввожу ЕЩЕ ОДИН НЕИЗВЕСТНЫЙ параметр t, так что
x2 = 8*t;
x1 = 3*t;
Тогда 18 = a*t^2*(3^2); 128 = a*t^2*(8^2);
то есть a*t^2 = 2 (вот как бывает:
Осталось найти, как x0 выражено через t;
(x0 - 3*t)/(8*t - x0) = 2/3;
5*x0 = 25*t;
x0 = 5*t;
y(x0) = 2*5^2 = 50;