Даны вершины треугольника A( 3; 7; -4), B( 5; -3; 2), C( 1; 3; -10).
1) Определяем векторы: АВ(2; -10; 6), ВС(-4; 6; -12) и АС(-2; -4; -6).
cos B = |-8-60-72|/√(4+100+36)*√(16+36+144) = 110/(√140*√196) = = 110/165,6502 = 0,84515.
Угол В = 0,5639 радиан = 32,3115 градуса.
cos А = |-4+40-36|/√(4+100+36)*√(4+16+36) = 0/(√140*√56) = 0.
Угол А = (π/2) радиан = 90 градусов.
cos С = |8-24+72|/√16+36+144)*√(4+16+36) = 56/(√140*√196) =
= 56/104,766407 = 0,53452.
Угол С = 1,00685 радиан = 57,6885 градуса.
2) Находим длины сторон.
Основания А1 3 0 -4
В1 2 5 -7
С1 4 2 -1
Длины АА1 7
медиан ВВ1 12,40967365
СС1 9,539392014
3) Длины АВ 11,83215957
сторон ВС 14
АС 7,483314774
Периметр равен сумме сторон: 33,31547434 .
4) Площадь можно найти двумя
- по формуле Герона,
- по модулю векторного произведения.
По Герону: p p-a p-b p-c
16,65773717 2,65773717 9,174422396 4,825577604
Площадь равна √1960 = 44,27188724 кв.ед.
Найдём расстояния между точками, это и будут стороны треугольника.
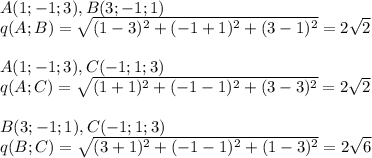
Три точки всегда лежат только в одной плоскости, задача свелась к обычной планиметрии, мы знаем три стороны треугольника. Надо найти углы, периметр и площадь.
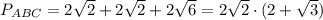
H∈BC; AH⊥BC; ΔABC - равнобедренный, поэтому высота будет и медианой, и биссектрисой.
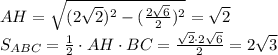
В прямоугольном ΔAHC, катет AH в два раза меньше гипотенузы AC, поэтому угол лежащий напротив катета AH равен 30°, то есть ∠С = 30°.
∠B = ∠C = 30°. ∠A = 180° - 30° - 30° = 120°.
ответ: ∠A = 120°; ∠B = 30°; ∠C = 30°;
Периметр: 2√2 · (2+√3);
Площадь: 2√3.
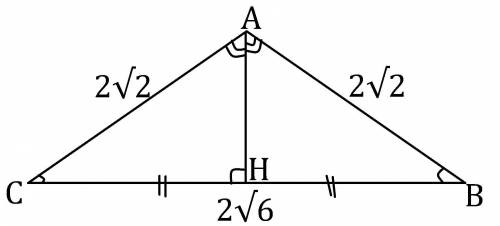
образуется 8 углов - по 4 в каждой точке пересечения: 1 - 4 и 5 - 8 смежные и вертикальные. Группы из 4 углов связаны между собой углами 3 и 6, 4 и 5 - накрест лежащие и 3 и 5, 4 и 6 - односторонние.
вертикальные и накрест лежащие равны между собой, а смежные и односторонние в сумме равны 180°.
Так как нам даны разные углы, то это углы смежные или односторонние. Таким образом, можем записать, что градусные меры этих углов относятся как 1:5, то есть в сумме равны 1х+5х=6х =180°. Отсюда х=30°.Пусть <2=x=30°. Тогда <1= 150°.
ответ: <1,<4,<5,<8 =150°, а <2,<3,<6,<7 = 30°
2. В условии явная ошибка. Должно быть: "Докажите, что биссектриса ВN угла СВД (Д лежит на прямой АВ), смежного с углом В треугольника, параллельна АС" , так как точки А,В, и D лежат на одной прямой, а биссектриса BN пересекает эту прямую.
Решение.
Угол А при основании АВ равен 60°, следовательно и <B =60°. Смежный с этим углом <CBD = 180°-60°=120°, а биссектриса BN делит его пополам. Следовательно, <NBD=60° и он равен <A, а это соответственные углы при прямых АС и BN и секущей АD. Значит
прямые АС и BN параллельны, что и требовалось доказать.
3. Треугольники MOS и NOP, MON и POS попарно равны по двум сторонам и углу между ними (равенство сторон дано, а углы - вертикальные).
Из равенства треугольников следует равенство сторон MS и NP,
MN и PS. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник - параллелограмм и MS||MP, а MN||PS, что и требовалось доказать.