[ Решение] Пусть ABCD-параллелограмм
с перпердикулярными диагоналями и О— точка пересечения диагоналей
Треугольники AOB и AOD равны
первому признаку равенства
треугольников. У
углы при вершине О по
по условию прямые,
сторона АО общая, OB=OD
по свойству диагоналей параллелограмма. Из равенства треугольников следует равенство
сторон AB=AD. А по свойству противолежащих сторон
параллелограмма AD=BC, AB=CD.
Итак, все стороны параллелограмма равны, а значит,
он есть ромб.
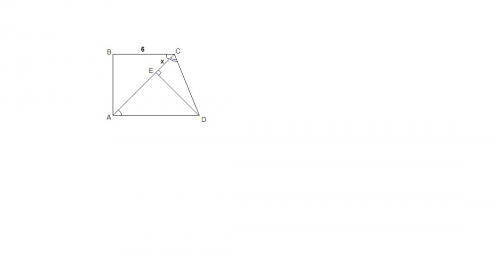
∠АСВ = 45°
∠CAD = ∠ACB = 45° как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АС.
Тангенс угла ACD положительный, значит этот угол острый, тогда треугольник ACD остроугольный и высота DE лежит внутри треугольника.
ΔAED: ∠AED = 90°, ∠EAD = 45°, ⇒ треугольник равнобедренный,
AE = ED.
Пусть СЕ = х, тогда АЕ = ED = 6√2 - х.
ΔCED: tg∠ECD = ED/CE
2 = (6√2 - x) / x
2x = 6√2 - x
3x = 6√2
x = 2√2
CE = 2√2 см