PΔABC ≈ 27.91
Объяснение:
Чтобы найти периметр треугольника, надо сначала найти длину каждой стороны треугольника, в этом нам формула квадрата расстояния между двумя точками в пространстве, или можно взять формулу модуля вектора, кому как удобно...
AB² = (x₁ - x₂)² + (y₁ - y₂)² + (z₁ - z₂)² ;
AB² = (2 - 3)² + (4 + 5)² + (-2 - 1)² = (-1)² + 9² + (-3)² = 1+81+9 = 1
AB = √91 ≈ 9,54;
BC² = (3 + 2)² + (-5 - 3)² + (1 - 5)² = 5² + (-8)² + (-4)² = 25+64+16 = 105
BC = √105 ≈ 10,25;
AC² = (2 + 2)² + (4 - 3)² + (-2 - 5)² = 4² + 1² + (-7)² = 16+1+49 = 66
AC = √66 ≈ 8,12
PΔABC ≈ 9,54 + 10,25 + 8,12 ≈ 27.91
Построение:
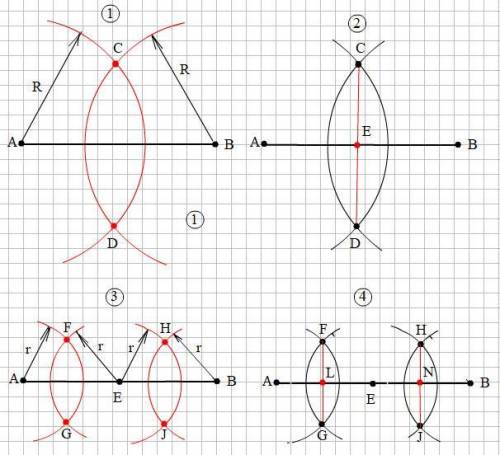
Смотри рисунок на прикреплённом фото.
Дан отрезок АВ.
1. Из точек А и В радиусом R > 0,5 AB проводим дуги, пересесекающиеся в точках C и D.
2. Соединяем точки С и D прямой, пересекающей отрезок АВ в точке Е. Е - середина отрезка АВ. Мы разделили отрезок АВ на две равные части.
3. Из точек А и Е радиусом r < 0,5 АЕ проводим дуги, пересекающиеся в точках F и G. Из точек B и Е радиусом r < 0,5 BЕ проводим дуги, пересекающиеся в точках H и J.
4. Соединяем точки F и G прямой, пересекающей отрезок АВ в точке L. Точка L - середина отрезка AE. Мы разделили отрезок АE на две равные части. Соединяем точки H и J прямой, пересекающей отрезок АВ в точке N. Точка N - середина отрезка ВE. Мы разделили отрезок ВE на две равные части.
Точки Е, L и N делят отрезок АВ на 4 равные части.
ΔАВС - прямоугольный (∠С = 90°).
cos(∠А) = 0,4.
АС = 12 см.
Найти :АВ = ?
Решение :Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.Следовательно, cos(∠А) = АС/АВ.
АС/AB = 0,4
12 см/АВ = 0,4
АВ = 12 см : 0,4 = 30 см.
ответ :30 см.