Подробно.
Пусть данный ромб АВСД.
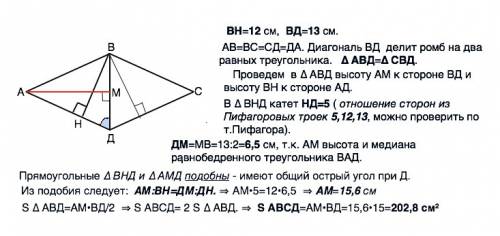
Высота ВН=12 см, диагональ ВД=13 см.
Стороны ромба равны.
Диагональ ромба делит его на два равных треугольника.
∆ АВД=∆ СВД.
Проведем в равнобедренном ∆ АВД высоту АМ к стороне ВД и высоту ВН к стороне АД.
В ∆ ВНД катет НД=5 ( отношение сторон из Пифагоровых троек 5,12,13, можно проверить по т.Пифагора).
ДМ=МВ=13:2=6,5 см, т.к. АМ высота и медиана равнобедренного треугольника ВАД.
Прямоугольные ∆ ВНД и ∆ АМД подобны - имеют общий острый угол при Д.
Из подобия следует:
АМ:ВН=ДM:ДH.
АМ•5=12•6,5
AM=15,6 см
S ∆ АВД=АМ•ВД/2
S АВСД= 2 S ∆ АВД.
S АВСД=АМ•ВД=15,6•15=202,8 см²
Сначала проверяем, подобны ли данные треугольники, если они подобны, то соотношение соответственных сторон должно быть правильным, значит:
АС/А₁С₁=ВС/В₁С₁
4/6=12/18
4*18=6*12
72=72 значит треугольники подобны
Тогда составляем пропорцию с неизвестной стороной А₁В₁:
АВ/АС=А₁В₁/А₁С₁
10/4=А₁В₁/12
А₁В₁=10*12/4=30
Задача 2
Мы знаем что, площади подобных треугольников относятся как квадраты сходственных сторон., Значит:
18/288=9²/А₁В₁
А₁В₁=288*81/18=
Задача 3
Рассмотрим треугольники АОВ и ДОС, они подобны по первому признаку (когда два угла одного треугольника соответственно равны двум углам другого треугольника), так как ∠АОВ=∠ДОС как вертикальные, а ∠АВД=∠ВДС как внутренние накрест лежащие (так как АВ параллельно ДС, ведь АВСД трапеция и АВ и СД ее основания)
Тогда составляем пропорцию отношения сторон подобных треугольников:
ДО/ДС=ОВ/АВ
20/50=8/АВ
АВ=50*8/20=20
ответ АВ=20