Дано:
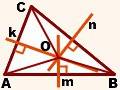
∆ ABC,
m, n, k — серединные перпендикуляры к сторонам AB, BC, AC
Доказать: m, n, k пересекаются в одной точке.
Доказательство:
Сначала докажем, что серединные перпендикуляры к двум сторонам треугольника пересекаются в одной точке.
Предположим, что m и k не пересекаются. Тогда m ∥ k.
Но прямые AB и AC пересекаются в точке A. Пришли к противоречию. Следовательно, прямые m и k пересекаются.
Обозначим точку пересечения прямых m и k как O.
По свойству серединного перпендикуляра к отрезку AO=OC и AO=BO. Следовательно, и OC=BO. Значит, точка O равноудалена от концов отрезка BC, следовательно, лежит на серединном перпендикуляре n к этому отрезку. Таким образом, все три серединных перпендикуляра m, n, k к сторонам треугольника ABC пересекаются в одной точке O.
Что и требовалось доказать.
Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной около этого треугольника окружности
(поскольку OA=OB=OC).
Точка пересечения серединных перпендикуляров к сторонам треугольника — одна из четырех замечательных точек треугольник
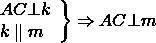
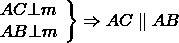
точка С
Объяснение:
АВ найбільший відрізок, який складається з двох маленьких АС і ВС, тобто АВ = АС + ВС, точка С ділить його на ці відрізки
Перевіримо: чи АВ = АС + ВС
19 = 12 + 7
19 = 19
рівність справджується , отже точка С лежить між точками А і В