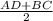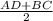* h * h =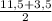 
* 7,5 = 56,25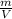
В треугольнике АВС сторона ВС = 4 см, ∠В = 25°, ∠С = 40°. Найти ∠А и стороны АВ, АС.
============================================================
Сумма всех углов в треугольнике равна 180°:∠А + ∠B + ∠C = 180°∠A = 180° - 25° - 40° = 180° - 65° = 115°По теореме синусов:BC/sin∠A = AB/sin∠C ; 4/sin115° = AB/sin40° ⇒AB = 4•sin40°/sin115° = 4•sin40°/cos25° ≈ 4•0,64/0,91 ≈ 2,56/0,91 ≈ 2,81 смBC/sin∠A = AC/sin∠B ; 4/cos25° = AC/sin25° ⇒AC = 4•sin25°/cos25° = 4•tg25° ≈ 4•0,47 ≈ 1,88 смОТВЕТ: ∠А = 115° , АВ ≈ 2,81 см , АС ≈ 1,88 см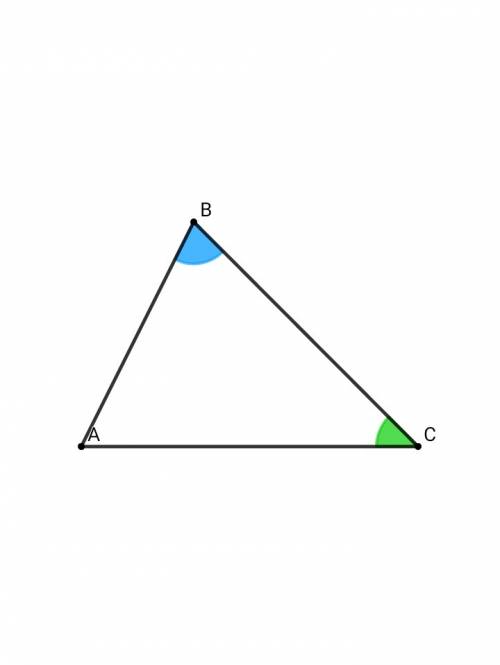
∠BAC = ∠ВА₁С₁ как соответственные при пересечении АС║А₁С₁ секущей ВА,
∠ВСА = ∠ВС₁А₁ как соответственные при пересечении АС║А₁С₁ секущей ВС,
угол при вершине В - общий для треугольников АВС и А₁ВС₁,
Значит все углы ΔАВС соответственно равны углам ΔА₁ВС₁.