Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.
Объяснение:
Вписанная в окружность трапеция является равнобедренной.
Значит АВ=CD стягивают равные дуги → ∪AB=∪CD
∠BOC=80° -центральный → ∪ВС=80°
∠AOD=100°--центральный → ∪АВD=100° ⇒ ∪AB=∪CD=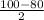 =10°.
=10°.
∠BAD вписанный и опирается на дугу ∪BCD=∪BC+∪CD=80°+10°=90°.
∠BAD=1/2*90°=45°. Значит ∠СDA=45° и ∠СВA=45° (углы при основании равны )
Сумма углов 4-х угольника 360°. Поэтому ∠АВС=∠ВСD=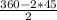 =135°
=135°
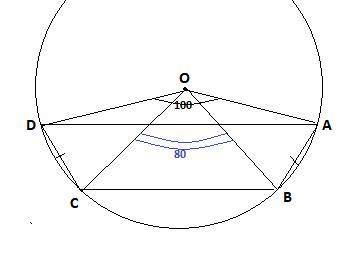
1) угол 1 = углу 4 т. к. они накрест лежащие при секущей DB
Угол 2 = углу 3 т. к. они накрест лежащие при секущей DB
Значит угол D = углу B, соответственно угол A = углу С, а в Параллелограмме противоположные углы равно, значит это параллелограмм
2)AD = CB, DC = AB, а в Параллелограмме противоположные углы равны значит это Параллелограмм
3)угол DBC = углу ADB - накрест лежащие
Угол ACD = углу BAC, значит угол А = углу С, а угол В = углу D, в Параллелограмме противоположные углы равны, значит это параллелограмм.
вот такой вот ответ,решать и понимать оч долго,