№1
S1=8*8=64
S2=15*15=225
S3=225+64=289
сторона третьего квадрата =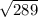 
= 17см.
№2.
Е
В О С
А Д
Что бы доказать, что площадь прямоугольника ABCД равна площади треугольника AEД, надо доказать, что площадь треугольника ЕВО=площади треугольникаОСД (т.е. треугольники равны), т.к. пдощадь АВСД=площадьАВОД+площадьОСД.
АВ=ВЕ (по построению)
АВ=СД (по св-вам прямоугольника)
следовательно ВЕ=СД
уголОЕВ=углуСДО (т.к. накрест лежащие для АЕ II СД и секущей ЕД)
угол ОСД=углуЕВО=90градусов
следовательно тр.ВЕО=тр.ОСД по стороне и двум прилежащим углам (по II признаку)
Что и требовалось доказать.
19
Объяснение:
1)Все три медианы должны пересекаться в одной точке. CP - это тоже медиана, потому что ВМ, АК и СР пересекаются в одной точке (О), где ВМ и АК - медианы.
СР - медиана, поэтому она делит сторону АВ на 2 равных отрезка - АР и РВ, равных 5. Одну сторону треугольника ОВР мы нашли - это сторона ВР = 5.
2) Все медианы в точке пересечения делятся в отношении 2:1, считая от вершины. Рассмотрим медиану СР.
Медиана СР = 18 (по условию).
Она делится в отношении 2:1 от вершины, то есть СО = 12, ОР=6.
Вторую сторону треугольника ОРВ мы нашли - ОР, она = 6.
3) Аналогично с медианой МВ.
ВО = 8, ОМ = 4.
Третья сторона треугольника ОВР найдена - ОВ, которая = 8.
4) Чтобы найти периметр треугольника, надо сложить все стороны.
Р = 8 + 6 +5 = 19 см.
∠BOA = 106°
∠COA = 108°
∠COB = 146°
Объяснение:
В треугольниках MOC и MOA:
MO - общая сторона, OC = OA - радиус вписанной окружности, ∠MCO=∠MAO=90°
а значит треугольники MOC и MOA равны (MA и MC равны, вычисляются по т. Пифагора. Поэтому треугольники равны по 3 сторонам)
Таким образом, ∠NMO = ∠LMO. Аналогично ∠MNO = ∠LNO.
Поэтому
∠NML = 2 * ∠NMO = 72°,
∠MNL = 2 * ∠ONL = 74°
Из 4-угольников ANBO и AMCO:
∠BOA = 360° - ∠OAN - ∠OBN - ∠ANB = 180° - 74° = 106°
∠AOC = 360° - ∠OAM - ∠OCM - ∠AMC = 180° - 72° = 108°
∠COB = 360° - ∠BOA - ∠AOC = 360° - 106° - 108° = 146°
1)
найдём площади обоих квадратов
8*8=64
15*15=225
64+225=289
V289=17
ОТВЕТ: 17
2 не знаю, прости...