1) Я долго сомневался, как лучше сделать, и все-таки решил не выводить здесь известные свойства внешних и внутренних касательных к двум окружностям. Просто перечислю то, что нужно знать для решения этой задачи. Найдите в учебниках или докажите сами.
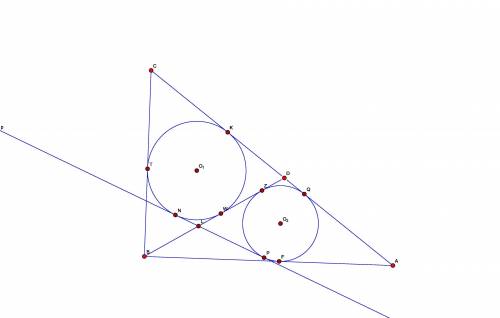
LD = NP = KQ;
кроме того, равны и "кусочки" этих отрезков:
LN = LW = DZ = DQ; DK = DW = LZ = LP;
(некоторые, я в том числе, испытывают серьезные трудности восприятия этих равенств, когда впервые с ними сталкиваются, особенно с учетом того, как просто они получаются)
2) BZ = BF = BL + LZ = BL + DK; аналогично BT = BW = BL + DQ;
=> BL + DK + BL + DQ + CT + AF + AC = 2p; (как всегда, p - полупериметр ABC)
CT + AF = AC - QK;
=> 2*BL + QK + 2*AC - QK = 2p;
=> BL = p - AC = (AB + BC - AC)/2 = 2; это в точности равно радиусу вписанной в ABC окружности.
В тр-ке ВОК=ВО=D/2=5√2, ВК=ВК/2=5, sin(ВОК)=ВК/ВО=5/5√2=√2/2.
∠ВОК=45°, ∠АОВ=90°.
∠ОАВ=∠ОВА=45°.
В оставшейся части окружности расположено пять равных тр-ков, градусная мера центрального угла каждого из них равна: ∠ВОС=(360-90)/5=54°. ∠ОВС=(180-54)/2=63°.
Градусная мера угла шестиугольника, образованного двумя равными треугольниками, равна сумме углов при основании одного из них.
∠ВСД=63+63=126°.
В шестиугольнике ∠С=∠Д=∠Е=∠Ф=126° - это ответ.
∠А=∠В=∠ОВА+∠ОВС=45+63=108° - это ответ.