
12 12 12 14 14
Объяснение:
1) рассм треуг АВС - равностор (по усл ), значит Р:3=36:3=12 стороны АВ ВС АС;
2) рассм треуг АДС - равнобедр (по усл) и АС =12, значит АД=СД= (Р-АС):2=(40-12):2=14;
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
168 кв ед
Объяснение:
1)Рассмотрим прямоугольный треугольник АВН(<Н=90°)
<В=90°-45°=45° => треугольник АВН - равнобедренный. АН=ВН=24
Площадь прямоугольного треугольника равна половине произведения его катетов :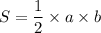
а=АН=24, b=ВН=24
тогда площадь треугольника АВН равна:
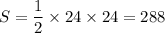
2)Рассмотрим прямоугольный треугольник CВН(<Н=90°)
По теореме Пифагора найдём катет СН:
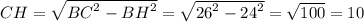
Площадь треугольника СВН(катет а=СН=10, катет b=ВН=24):
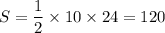
Площадь треугольника ABC равна разности площадей треугольников АВН и СВН:
S(ABC)=S(ABH)-S(CBH)=288-120=168 кв ед.
Треугольник АВС
Высота ВН делит его на два прямоугольных треугольника АВН и СВН, где АВ и ВС - гипотенузы.
Примем АН за х.
Тогда СН = АС-х
Составляем два уравнения:
Для треугольника АВН:
ВН^2 = АВ^2 - х^2
Для треугольника СВН:
ВН^2 = ВС^2 - (АС -х)^2
Так как левые части этих уравнений равны, то равны и правые.
АВ^2 - х^2 = ВС^2 - (АС -х)^2
АВ^2 - х^2 - ВС^2 + АС^2 -2АС•х + х^2 = 0
2х•АС = АВ^2 - ВС^2 + АС^2
х = (АВ^2 - ВС^2 + АС^2) / 2АС
Тогда значение х можно вставить в уравнение:
ВН^2 = АВ^2 - х^2
ВЕ^2 = АВ^2 - ((АВ^2 - ВС^2 + АС^2) / 2АС)^2
Объяснение:
AB = 12 AC = 12 BC = 12,
AD = 14 DC = 14.