ответ: S=20см²
Объяснение:
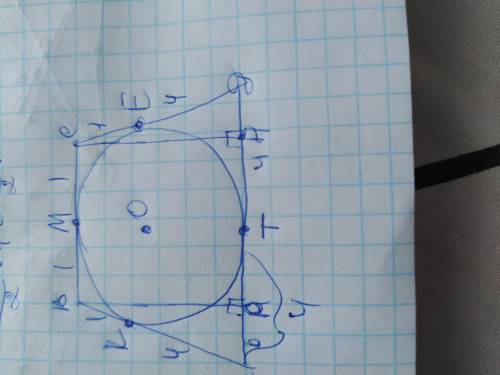
Обозначим вершины трапеции А В С Д а точки касания К М Е Т, а центр окружности О. Стороны трапеции являются касательными к вписанной окружности поэтому отрезки касательных соединяясь в одной вершине равны между собой от вершины до точки касания. Поэтому:
КВ=ВМ=МС=СЕ=1см. АК=АТ=ТД=ЕД=4см.
Из этого следует что:
АВ=СД=1+4=5см
ВС=1+1=2см
АД=4+4=8см.
Проведём из вершин трапеции В и С две высоты к основанию АД –ВР и СН. Они делят АД так, что РН=ВС=2см. Так как трапеция равнобедренная то АР=ДН=(8-2)/2=6÷2=3. Рассмотрим полученный ∆СДН. Он прямоугольный, в котором СН и ДН –катеты, а СД – гипотенуза. Найдём СН по теореме Пифагора: СН²=СД²-ДН²=
=5²-3²=25-9=16; СН=√16=4
СН=4см
Теперь найдём площадь трапеции зная высоту и основания по формуле:
S=(BC+AD)/2×CH=(2+8)/2×3=10/2×4=
=5×4=20см²
В прямоугольном треугольнике
синус острого угла - отношение противолежащего катета к гипотенузе
косинус острого угла - отношение прилежащего катета к гипотенузе
тангенс острого угла - отношение противолежащего катета к прилежащему (или синуса к косинусу)
cosA =AC/AB =sinB =1/2
Пусть AC=x, AB=2x
По теореме Пифагора
BC =√(AB^2 -AC^2) =x√(4-1) =x√3
tgA =BC/AC =√3
Или
cosA =cos(90-B) =sinB =1/2
sinA^2 +cosA^2 =1 => |:cosA^2
tgA^2 +1 =1/cosA^2 =>
tgA = +-√(1/cosA^2 -1) = +√(4-1) =√3
(тангенс острого угла положительный)