АА1 = 6 см.
Объяснение:
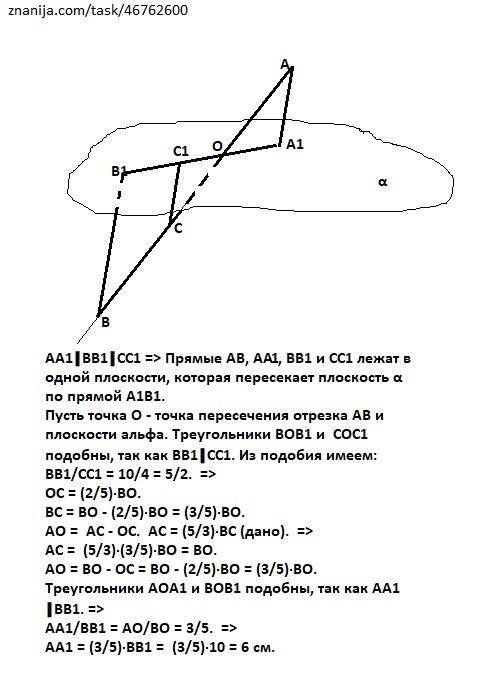
АА1║ВВ1║СС1 => Прямые АВ, АА1, ВВ1 и СС1 лежат в одной плоскости, которая пересекает плоскость α по прямой А1В1.
Пусть точка О - точка пересечения отрезка АВ и плоскости альфа. Треугольники ВОВ1 и СОС1 подобны, так как ВВ1║СС1. Из подобия имеем: ВВ1/СС1 = 10/4 = 5/2. =>
ОС = (2/5)·ВО.
ВС = ВО - (2/5)·ВО = (3/5)·ВО.
АО = АС - ОС. АС = (5/3)·ВС (дано). =>
АС = (5/3)·(3/5)·ВО = ВО.
АО = ВО - ОС = ВО - (2/5)·ВО = (3/5)·ВО.
Треугольники АОА1 и ВОВ1 подобны, так как АА1║ВВ1. =>
АА1/ВВ1 = АО/ВО = 3/5. =>
АА1 = (3/5)·ВВ1 = (3/5)·10 = 6 см.
Sin²a+Cos²a=1
Sina=√1-Cos²=√1-(2√2/3)²=√1-8/9=√1/9=1/3
SinA=BC/AB ⇒ AB=BC/SinA
AB=2/(1/3)=6
сторона AB равна 6