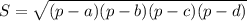Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как:
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны:
Линейный угол двугранного угла --это угол между перпендикулярами, лежащими в гранях угла, опущенными на линию пересечения плоскостей=граней двугранного угла (на ребро двугранного угла) по построению AH _|_ (a), BH _|_ (a), угол АНВ = 60° ----------------------------------------------------------------------------- расстояние от точки Т до плоскости (грани двугранного угла) --это перпендикуляр из точки на плоскость ТВ _|_ (альфа) ---> TB _|_ BH аналогично, TA _|_ AH TA=TB по условию ----------------------------- TH --это будет расстояние от точки до прямой (тоже перпендикуляр))) TH _|_ (a) по теореме о трех перпендикулярах ТН=10 по условию ----------------------------- точка, равноудаленная от сторон угла лежит на биссектрисе угла угол ТНВ=30° катет, лежащий против угла в 30 градусов равен половине гипотенузы))) ТВ=ТА=5
16.
а)
Диагональ BD — делит четырёхугольник на 2 произвольных треугольника: ΔBCD; ΔBAD.
Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как:
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны: