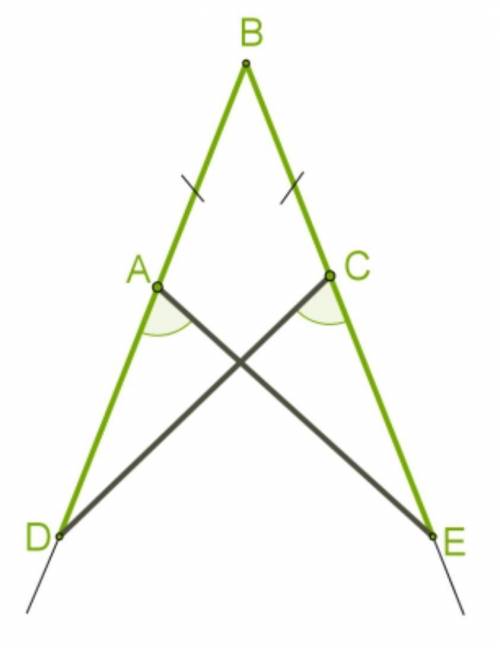
PP1Q1Q-квадрат
Периметр равен 41,2 см
Объяснение:
Две прямые, перпендикулярные одной и той же плоскости, параллельны.PP1 ⊥ 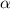 ,
,
QQ1 ⊥ 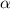 => PP1 II QQ1
=> PP1 II QQ1
PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.=>PQ II P1Q1
PQQ1P1 - параллелограмм.
Так как < PP1Q1, <QQ1P1 равны 90°, то
PQQ1P1 - прямоугольник.
PP1=PQ => PQQ1P1 - квадрат.
Периметр квадрата находится по формуле:
Р=4а=4×10,3= 41,2 см
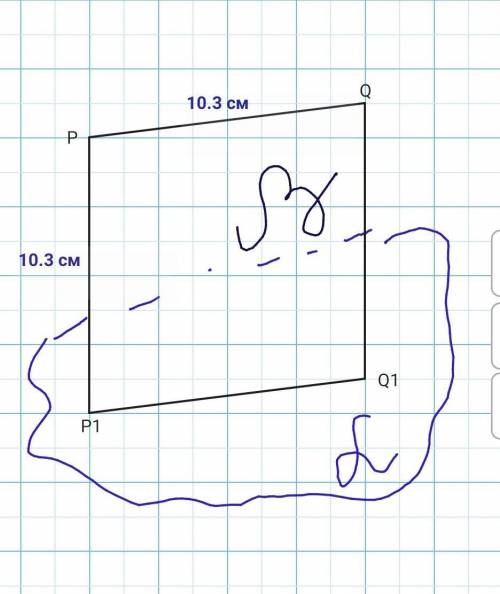
Треугольник BDE равнобедренный так как стороны BD и BE равны из условия. Значит угол ADE равен углу CED. Рассмотрим треугольники ADE и CED. Они подобны и равны друг другу так как две строны: AD = CE и DE = ED и угол между ними (угол ADE = углу CDE) равны. Так как треугольники равны то и угол DCE = углу EAD.